Radiometry involves measuring and predicting levels of optical radiation. This article removes some of the confusion surrounding this often complex technology.
Angelo V. Arecchi, Labsphere, Inc.
Radiometry involves several activities. The two most common are the description and measurement of optical radiation, and, starting with the knowledge of some aspects of optical radiation at one location, predicting the measurement that would be made at another.
This article will concentrate on the description and measurement of light.
A complete description of the light from a source could be extremely complex, involving spatial (at least two, sometimes three dimensions), angular (generally two or more dimensions), and spectral and temporal dimensions. This leaves out concepts such as polarization and coherence, which are commonly discussed outside the subject of radiometry, but can be important here, too. The usual practice in radiometry is to simplify the possibilities and work with only a few specific geometric and spectral concepts. We’ll concentrate on the most common of these concepts, talk about how to choose the appropriate one for a specific situation, and discuss how to make meaningful measurements.
Any device that responds to light and produces a measurable output can be used as a radiometer. The most common radiometric detectors produce changes in their electrical properties (generally current, voltage or resistance) or their temperature, which is then measured electrically. In most cases, the output of the detector is connected to a display that is calibrated to read out the amount of light absorbed by the detector.
TABLE 1.
GEOMETRIC AND SPECTRAL ASPECTS OF RADIOMETRY
SPECTRAL
| |
|
|
|
Radiometric |
|
Spectroradiometric |
|
Photopic |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
Power |
|
Power/wavelength interval |
|
Luminous flux |
| |
|
Flux
|
|
|
|
|
|
|
| |
|
|
|
Watts |
|
Watts/nm |
|
Lumens |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
Irradiance |
|
Spectral irradiance |
|
Illuminance |
| |
|
Flux/Area |
|
|
|
|
|
|
|
|
|
|
Watts/m2 |
|
Watts/m2 x nm |
|
Lumens/m2 = lux |
| GEOMETRIC |
|
|
|
|
|
|
|
|
| |
|
|
|
Radiant intensity |
|
Spectral intensity |
|
Luminous intensity |
| |
|
Flux/Solid |
|
|
|
|
|
|
| |
|
Angle |
|
Watts/sr |
|
Watts/sr x nm |
|
Lumens/sr = candela |
| |
|
|
|
|
|
|
|
|
| |
|
|
|
Radiance |
|
Spectral radiance |
|
Luminance |
| |
|
Flux/Area |
|
|
|
|
|
|
| |
|
Solid Angle
|
|
Watts/m2 x sr |
|
Watts/m2 x sr x nm |
|
Candela/m2 = nit |
| |
|
|
|
|
|
|
|
Lumens/m2 sr = nit |
The geometric and spectral aspects of radiometry are almost always separable from each other, so it makes a lot of sense to discuss them independently. Table 1 shows such a separation for the most common radiometric quantities. The rows are identical geometrically but differ spectrally, while the columns share common spectral descriptions and vary in their geometry. The SI unit for each quantity is listed.
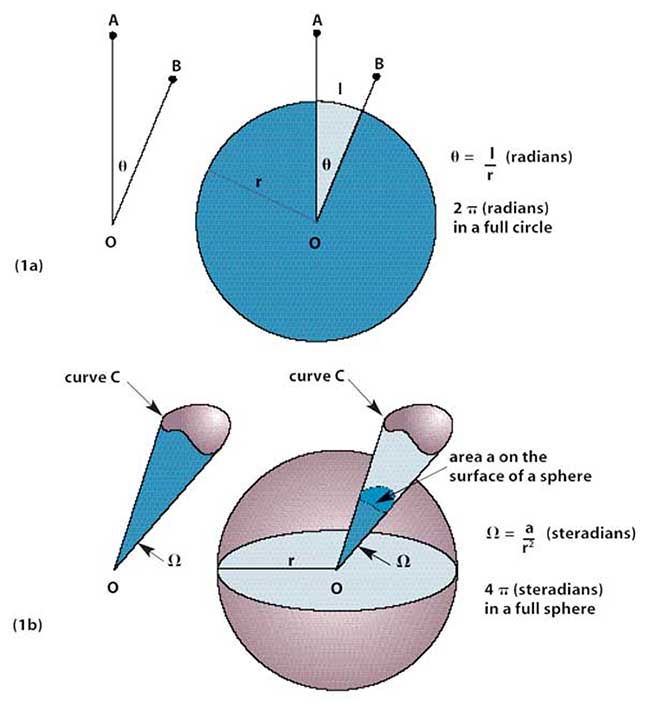
Figure 1. The concept of solid angle in three dimensions can be thought of as analogous to an ordinary plane angle in two dimensions. In 1a, the plane angle θ is formed by OA and OB and is measured by drawing a circle with an arbitrary radius r. The angle θ equals the length of arc l divided by r. In 1b, Ω is formed by the locus of all lines connecting O to the curve C. The solid angle Ω is measured by drawing a sphere of arbitrary radius r. The angle Ω equals the area a inscribed on the surface of the sphere divided by r2.
Geometry
The four most commonly used geometric descriptions in radiometry are flux, irradiance, intensity and radiance.
• Flux (watts): The total optical power emitted from a source in all directions. For example, the total amount of light emitted from a light bulb is its flux. Flux can be thought of as the fundamental quantity of radiometry; the other quantities defined here are geometric or spectral distributions of it.
• Irradiance (watts/m2): The flux impinging on a surface per unit of surface area. For example, the ability to read this page depends upon the amount of light falling on it, or the irradiance.
• Intensity (watts/sr): Radiant objects that are small, at least in comparison to the distance between them and the observer, can be treated for radiometric purposes as point sources. For these sources, the flux emitted per unit solid angle (Figure 1) is called the intensity. The measure of the ability of a flashlight to provide a lot of light onto a distant target is its intensity.
• Radiance (watts/m2 × sr): For extended radiant sources, think about the intensity per unit of projected area or, equivalently, the flux emitted per unit projected area per unit solid angle. This quantity is called the radiance. The visual perception of the brightness of an object is a response to its radiance. Like intensity, radiance can vary with the direction from the object to the observer. (An object that has constant radiance over all directions is called lambertian. A very matte piece of paper and the surface of a fluorescent light tube are good approximations of lambertian objects.)
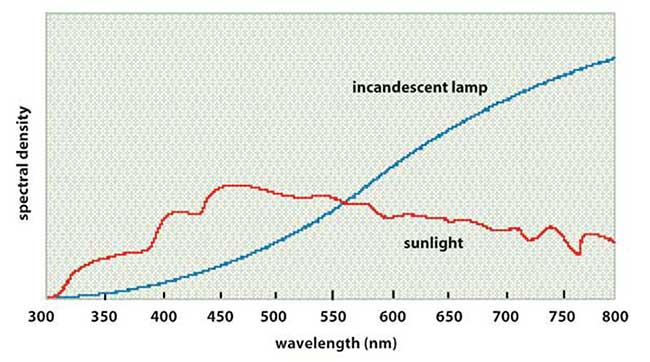
Figure 2. The spectrum of sunlight peaks at about 450 nm, while that of an incandescent lamp peaks at more than 800 nm.
Spectrum
• Spectroradiometric flux (watts/ nm): Generally, optical radiation refers to that slice of the electromagnetic spectrum from about 200 nm to 20 µm. The spectrum of a particular light source is represented by its spectral density, in units of power per wavelength interval. Figure 2 shows the typical spectral densities of two common light sources.
• Blackbodies: Many items when heated produce optical radiation with a specific spectral shape that depends solely on the temperature. These are called blackbodies. When heated to high enough temperatures, items such as electric stove elements and light bulb filaments can produce enough visible light to be seen or even to illuminate a room. Figure 3 shows the normalized spectral densities of blackbodies of several temperatures.
• Total flux (watts): Total flux in a specified spectral band is found by integrating the spectral density over the band.
• Luminous flux (lumens): The response of the human eye to radiometric flux can be predicted by calculating the luminous flux. This is attained by multiplying the spectroradiometric flux by the luminous efficacy curve (Figure 4), and integrating the product.
• Color: The perceived color of a light source is the result of mostly biological and psychological processes. However, there is an accepted engineering model of the human color vision system. With this model, the perceived color of a light source can be described by a pair of numbers called chromaticity coordinates. In general, an infinite number of possible spectra can produce the same pair of color coordinates.
• Color temperature: Any light source, although spectrally different from a blackbody, that has the same chromaticity coordinates as one, can be described as having the color temperature of the blackbody.
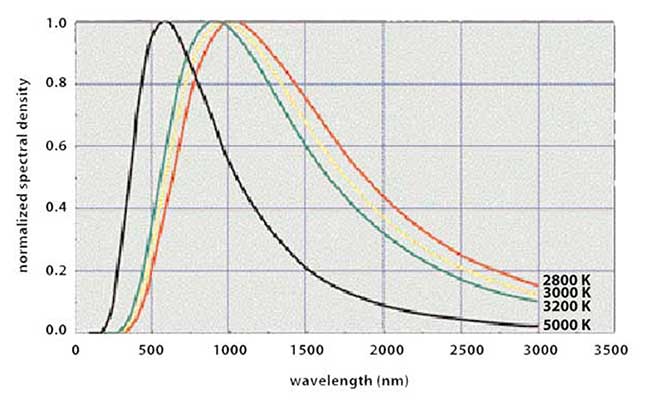
Figure 3. The spectral density of blackbodies varies with temperature.
Radiometric measurements
• Flux: The total flux from a source is usually measured in an integrating sphere. The combination of sphere and radiometer is calibrated on a periodic basis using a reference source of known output flux.
• Irradiance: If the source of radiation is far enough away from the region where the irradiance is to be measured that the light is very collimated, then a detector alone is sufficient. If the irradiance comes from a broad source, such as a skylight or room light, then a diffuser must be placed in front of the detector. (A diffuser/detector combination also can be used in collimated light.) Most instruments designed for irradiance measurement come equipped with detectors calibrated to read directly in units of irradiance.
• Intensity: This usually is determined with a radiometer that actually measures irradiance. The intensity is calculated from the irradiance and the distance between the source and the irradiance detector as follows:
intensity = irradiance × (distance)2
• Radiance: A commercial imaging spot meter is the most common method of measuring radiance. Most spot meters are capable of simultaneously viewing the spot that is being measured, and usually read out directly in units of radiance.
• Spectrum: Radiometers that measure luminous flux (called photometers) usually are equipped with a glass or plastic filter in front of the detector. The combination of the filter and the detector provides a spectral response that approximates the shape of the luminous efficacy curve.
For narrowband sources, the responsivity of the detector is nearly constant over the band of the source, so a radiometer can be calibrated to read watts directly. Also, some detectors, especially thermal detectors, have a responsivity that does not vary with wavelength. These detectors read directly in watts, even for broadband sources. Unfortunately, thermal detectors are not always suitable for all applications.
The spectral character of a source is measured with a device called a spectroradiometer, which can be outfitted with input optics to measure spectral flux, spectral irradiance or spectral radiance.
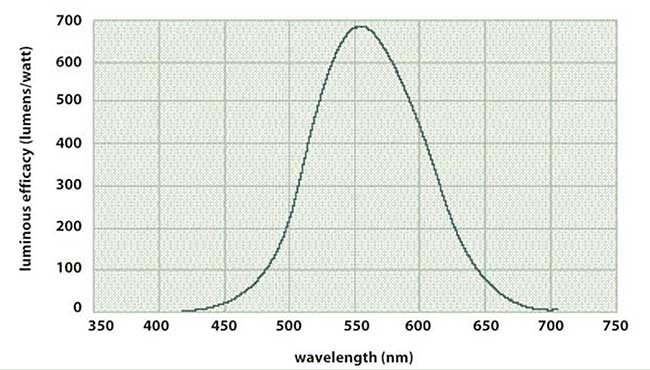
Figure 4. Luminous efficacy peaks at approximately 555 nm.
Tips and pitfalls
• Whenever possible, convert all quantities into SI units and stay in SI units.
• Ensure that your radiometer actually measures the quantity that you intend to measure. Ensure that the quantity you intend to measure is the quantity you really need to measure.
• Table 1 breaks up the most common radiometric measurements into twelve distinct cells, four geometric rows and three spectral columns. A method of simplifying radiometry is to know which of the twelve boxes you are working in, and to also know when you’re not in any one of them, requiring a more involved description.
• The term intensity, unfortunately, also is used in related disciplines to mean something quite different from flux per unit solid angle. For example, physicists have long assigned this same word to mean any quantity that is proportional to power. Be sure to check the context for the intended meaning.
• Intensity and radiance are functions of direction. Irradiance, on the other hand, is not directionally dependent. It does not discriminate, for example, between very collimated light and light that is impinging from all angles.
• Intensity and radiance are properties of a source and are independent of the distance to the observer or the object being illuminated. Irradiance depends both on the properties of the source and on the distance to the object being illuminated.
• Radiance describes the light leaving a surface; irradiance describes light impinging on a surface. For a perfect reflecting diffuser (an unachievable surface that is 100 percent reflecting and perfectly lambertian), the radiance is equal to the irradiance divided by π (in SI units). For all real materials, there is no established relationship between radiance and irradiance. The relationship depends on the material and, generally, upon the angular distribution of the irradiance.
• The terms color temperature and blackbody temperature are not synonymous. Color temperature is derived from colorimetric calculations. While it is true, for example, that a blackbody of 3000 K has a color temperature of 3000 K, the converse may not be true. There are limitless spectra that possess a particular color temperature and have no resemblance to the blackbody curve for that temperature.
• For broadband sources, it does not make sense to talk about the flux at a single wavelength. The concept of flux makes sense only when discussed within a specified spectral band. The band may be determined by the source. For example, a 3000-K blackbody source has virtually all of its flux (99 percent) in the 300-nm to 8-µm band. The band may be specified by the application or by the detector, or selected with a filter.
• Sometimes, for very spectrally narrow sources such as lasers, it is common to speak of the power at the laser wavelength. It’s more accurate instead to speak of the laser power being contained in a narrow band around that wavelength.
Recommended reading
Arecchi, A.V., Messadi, T., and Koshel, R.J. (2007). Field Guide to Illumination. SPIE Press,
Bellingham, Wash.
Bartell, F.O. (1989). APPLIED OPTICS, Vol. 28, No. 6.
De Cusatis, C., Ed. (1997). Handbook of Applied Photometry, AIP Press, Woodbury, N.Y.
McCluney, W.R. (1994). Introduction to Radiometry and Photometry, Artech House,
Boston and London.
Smith, W.J. (2007). Modern Optical Engineering, 4th Ed., SPIE Press, McGraw-Hill, New York.
Wolfe, W.L. (1998). Introduction to Radiometry, SPIE Press, Bellingham, Wash.