
Photometry: The Answer to How Light Is Perceived
Simply put, photometry is the measurement of visible light based on the response of the average human observer. How that definition translates into technically correct quantification methods is the focus of this article.
Photo Research, Inc.
That portion of the spectrum that the eye can see — and its rainbow of colors — is rather small, covering approximately 360 to 830 nm. What colors we perceive depends on wavelength, while the amount of light energy detected by the eye at a particular wavelength determines the perceived intensity of that color. In quantifying that energy, we use what is called radiant flux, a measure in watts, of the energy per second (or power) radiated from a source.
The visible spectrum covers the wavelengths from approximately 360 to 800 nm.
Radiated optical energy (light) can be measured and correlated with human vision. This is called photometry, which is defined as the measurement of visible light based on the response of an average human observer.
Who’s average?
The eye’s response to light depends on physical, physiological and psychological factors and varies from person to person, making it difficult to define the average observer. In 1924, the Commission Internationale de l’Eclairage (CIE), or International Commission on Illumination, conducted a series of experiments to quantify the human eye’s response to visible light. The result: a specified spectral luminous efficiency function V (λ) to characterize the daylight vision of the average human observer. This is now commonly known as the photopic function. Because the response changes at low light levels, the CIE also defined a scotopic function V’(λ) to characterize the response of the dark-adapted eye.
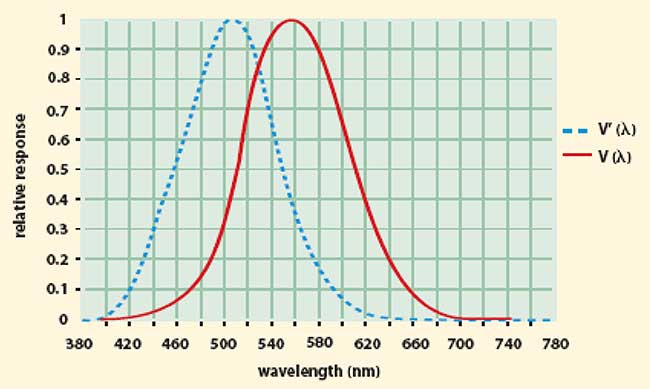
Figure 1. The response of two types of vision can be described by photopic (solid red) and scotopic (dotted blue) response curves.
Figure 1 shows the response at different wavelengths for both the normalized photopic and scotopic functions. The spectral response is greatest in the green region from 540 to 560 nm. Most people cannot see blue below 400 nm or red above 700 nm, so the photopic response is almost zero in these regions. The scotopic response peaks more towards the blue region for two reasons: for the dark-adapted eye, the color receptors or cone cells shut down, leaving the monochromatic rod cells as the primary sensors; and the production of rhodopsin — a purplish liquid that enhances night vision.
Luminous flux
The fundamental quantity used in photometry is luminous flux, which is the visible light energy per second radiated by a source or amount of photometric energy traveling through space in a given time interval. The lumen is the unit of luminous flux, and 1 W of radiant flux at the peak photopic wavelength of 555 nm is equivalent to a luminous flux of 683 lumens. If the radiant flux (power) of a polychromatic light source at every wavelength of the visible spectrum from the blue to the red end is known, the luminous flux can be calculated by mathematically integrating the power values with the CIE-defined photopic value for each wavelength.
For historical reasons, the candela — the unit of luminous intensity — takes precedence over the lumen. The candela originally was derived from the light emitted by a candle; its current definition is the luminous intensity, in a given direction, of a source that emits monochromatic radiation of frequency 540 × 1012 Hz and that has a radiant intensity in that direction of 1/683 W per steradian (540 × 1012 Hz is equivalent to 555 nm). The lumen is the luminous flux, emitted per unit solid angle from a point source whose luminous intensity is one candela. The unit of solid angle is the steradian (Figure 2), and because the surface area subtended by a steradian is r2, a sphere with a surface area of 4πr2 must have 4π steradians. Therefore, the total luminous flux emitted from a one-candela point source is 4π lumens.
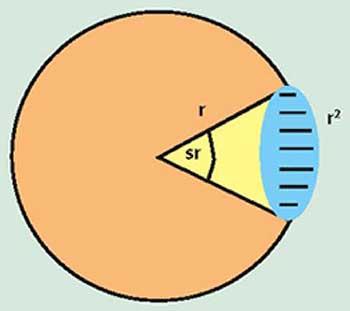
Figure 2. The steradian is the solid angle at the center of a sphere that subtends a surface area of r2.
Typically, lamp manufacturers measure the total lumen output by placing a photometer at the exit port of an integrating sphere. The lamps are placed inside the integrating sphere — a highly reflective sphere with a white, spectrally nonselective coating. Integrating spheres used for measuring large lamps can be up to 2 m in size. These devices also are used to measure directional sources such as laser beams and light-emitting diodes (LEDs).
Luminous intensity
Luminous intensity, or candlepower, is the luminous flux per unit solid angle emitted by a uniform point source of light. This is the quantity used to measure the output of point (small) sources such as LEDs and miniature lamps. The unit of luminous intensity is the candela, and it is given in lumens per steradian.
In many practical applications, point sources are directional and do not radiate uniformly. Therefore, candlepower is measured in a specific direction over a small collection angle along the axis of radiation. LED receptors, which use the technique to measure LEDs in millicandelas, consist of tubes with baffles that have a specific collections geometry (2° to 15° are common). The CIE has recommended in CIE 127 that LEDs be measured using 2° and 6.5° geometry, and that these two readings are averaged to yield "Averaged LED Intensity." A typical LED receptor is a tube in which one end is attached to the light measuring device and the other end receives the LED. The collection geometry is defined by a field stop in the tube. The receptor is then calibrated using a source of known luminous intensity.
Illuminance
Illuminance is measured whenever the light level at a particular surface has to be specified. For example, these measurements are required to characterize the light falling on a projector screen or to design light fixtures in a building. This is analogous to the luminous flux falling on a surface per unit area, and it is measured in lumens per unit area. The English system measures illuminance in lumens per square foot (footcandles), and the metric system uses lumens per square meter (lux). The conversion is 1 lux = 0.0929 fc.
Two laws of physics that affect illuminance measurements are the inverse square law and the cosine law. The inverse square law states that the intensity per unit area of a surface varies inversely with the square of the distance between the light source and the detector. Therefore, if illuminance is measured at a particular distance from a source, it is possible to calculate the illuminance at other distances.
The cosine law states that the illumination of a surface decreases as a function of the cosine of the incident angle of illumination. This happens because, as the angle of illumination is moved away from the perpendicular to the surface, the area of illumination increases and the flux density per area decreases. Shining a flashlight on a piece of paper at different angles will clearly illustrate this. Illuminance meters use a cosine diffuser that lights and weighs each ambient source’s flux density by the cosine of the angle at which it illuminates the surface, therefore providing cosine corrected results.
Luminance
Luminance, the most commonly measured photometric quantity, is required whenever it is necessary to know the apparent brightness of an object. Luminance is the luminous flux emitted from a surface or extended source per unit solid angle per unit area in a given direction and is, therefore, the luminous intensity per unit area. Luminance measurements are constant, regardless of the distance between the source and the detector because, as the intensity measured by a detector decreases with distance, the area of the measuring field increases proportionately.
Usually, a luminance meter has a lens to restrict the field of view of the detector. The human eye is the best-known example of a luminance meter. The unit of luminance is the footlambert (fl) in English units or the candela per square meter (cd/m2) in metric units. The metric unit was also previously known as the nit. The conversion factor is 1 cd/m2 = 0.2919 fl.
Common luminance meter applications are measuring extended sources such as cathode-ray tubes (CRTs), LCDs and PDPs and the reflectance of illuminated surfaces.
TABLE 1.
PHOTOMETRIC AND RADIOMETRIC UNITS
|
Radiometric Term |
|
Unit |
|
Photometric Term |
|
SI Unit |
|
English Unit |
| |
Radiant flux |
|
Watt |
|
Luminous flux |
|
Lumen |
|
Lumen |
| |
Radiant intensity |
|
Watt/steradian |
|
Luminous intensity |
|
Candela |
|
Candela |
| |
Radiance |
|
Watt/steradian/m2 |
|
Lumiance |
|
cd/m2 |
|
Footlambert |
| |
Irradiance |
|
Watt/m2 |
|
Illuminance |
|
Lux |
|
Footcandle |
A perfectly diffuse source has a lambertian surface and reflects light in all directions following the cosine law. A white piece of paper and a piece of opal glass are examples of good diffusers. If the luminance of a source is measured reflecting off a surface, it is possible to calculate the illuminance at that surface. It should be noted that when a perfectly diffuse surface is measured, 1 fc = 1 fl and 1 lux = π cd/m2. Table 1 lists important radiometric quantities and units and their photometric equivalents.
Photometers
Photometric measurements are made with instruments called photometers. The devices function by collecting light through some kind of input optics, passing it through a spectral modifying filter and then measuring the light with a photosensitive detector. The filter is carefully trimmed to modify the detector response so that it matches the CIE photopic (or scotopic) function. The detector converts the incoming light energy into an electrical signal, which is then amplified and displayed. Because the filter/detector combination approximates the eye response, the measured electrical signal is a true measure of the light as perceived by a human observer.
Photometers range from inexpensive, handheld light meters used by amateur photographers to expensive spot photometers with narrow acceptance angle optics and sensitive photomultiplier tube detectors. A special kind of filter photometer is the imaging photometer (also known as a video photometer), which has a photopic filter in front of an imaging detector like a charge-coupled device (CCD) camera. An imaging photometer captures images and gives photometric and spatial information for each of the camera’s pixels. Another advantage of imaging photometers is their ability to measure the photometric uniformity of a large area with a single camera image. This makes them useful for online inspection of products.
Various factors, such as the closeness of the photopic filter's match to the CIE V (λ) function, stray light and acceptance angle of the optics, linearity and stability of the detector and quality of the photometric calibration, have a significant impact on the performance of a photometer. The accuracy and repeatability of measurements also may depend on the spectrum of the source being measured, since the photopic filter in most photometers does not perfectly match the CIE V (λ) function accurately near the edges of the visible spectrum. Highly saturated sources such as cathode-ray tube phosphors, LEDs and discharge lamps pose challenges as their narrowband spectra differ significantly from the broadband incandescent sources used to calibrate most photometers. Errors caused by polarization and lens flare can seriously affect the measurement of liquid crystal displays.
Other critical selection factors are the range of sensitivity, ability to measure pulsed sources, portability, small-spot measurement capability, speed of measurement and ease of use. Today, many of the high-end photometers have built-in microprocessors and can perform completely automated measurements in seconds.
Spectroradiometers are another class of instruments that can be used to perform photometric measurements. A spectroradiometer measures the radiant flux of light at different wavelengths and then mathematically multiplies these spectral values with the CIE-defined photopic values at those wavelengths. By summing these multiplications at small wavelength intervals throughout the visible spectrum, a spectroradiometer accurately calculates photometric quantities. A good spectroradiometer can offer high accuracy for measuring any kind of light source, as there are no filters causing spectral mismatches. These instruments do not require special calibration factors for measuring narrowband LEDs, high-intensity discharge lamps, CRT phosphors, laser projectors, etc.
Photometry applications
Luminance meters are used in a number of industries to test the brightness of displays, instrument panels, night-vision devices, lamp sources, etc. The luminance of small characters on cockpit displays and instrument panels is tightly controlled in the aerospace and automotive industries by computerized quality control testing with spot photometers. Accurate and highly sensitive photometers are used to measure the contrast ratios of cathode-ray tubes, liquid crystal displays and other flat panel displays. In fact, sophisticated goniophotometers are used to characterize the luminance and contrast ratios of flat panel displays across a wide range of viewing angles.
Imaging photometers are used for fast and accurate uniformity testing of cockpit displays and automotive dashboards. They are suitable for ISO ergonomics testing of computer monitors since both photometric and spatial measurements have to be performed in this application. Illuminance of theater screens, uniformity of projection systems, transmittance of filters, and reflectance of paper, textiles and ceramics are other common photometric applications.
References
1. Stimson, A. Photometry and Radiometry for Engineers. Wiley-Interscience (1974).
2. CIE 41 — Light as a True Visual Quantity: Principles of Measurement. CIE, Vienna (1978).
3. Miller, K. How to Make Accurate Light Measurements. Photo Research, Chatsworth, Calif. (1985).
4. Nomenclatures and Definitions for Illuminating Engineering. IES, New York (1980).
5. CIE 127 Technical Report — Measurement of LEDs (1997).
/Buyers_Guide/Photo_Research_Inc/c11670