Dr. Michael E. Holmes, Toptica Photonics Inc., and Mohammad Mirhosseini and Dr. Robert Boyd, University of Rochester
When put into practical use, slow-light-enhanced technologies will improve the performance of photonic networks and optical sensors. Photonic crystals will play a key role in the transition, as they hold promise for integration into nanophotonic circuits.
Slow light enables the modification of the group velocity of photons in a controllable fashion. Although still a valuable research tool for physicists, slow light is slowly moving out of the research laboratory and into practical applications. Slow-light-enhanced technologies are expected to improve the performance of photonic networks and optical sensors. Photonic crystals (PhCs) are promising structures for integration into nanophotonic circuits for guiding and controlling light, and can also be engineered with large dispersive effects for optimal enhancement. To date, there are no commercial systems that directly take advantage of slow light or that are designed for this operation. However, patents exist with practical sensing in mind. This potentially will pave the way for integration into next-generation optical products.
Growing interest in miniature components for industrial and medical applications such as telecommunications and biosensing has guided recent advances in applied research in optics. Slow light1-3has a rich history of fundamental research and still fascinates scientists across many disciplines. Further, it provides a promising tool for designing ultracompact, high-precision spectral sensors for real-time detection. The concept of slow light is based on the rapid change of the refractive index associated with absorption features in material systems. It can be most easily understood by using Kramers-Kronig theory. In Figure 1, (a) shows a typical absorption profile that leads to (b) a rapid change in refractive index, and hence (c) to large changes in the group index ng, thus creating the conditions for slow and fast light. This process leads to large positive and negative values of the group velocity Vg, the speed with which pulses propagate through a medium. Here, Vg = c/ng, where c is the speed of light in vacuum. We focus on large positive group indices such that Vg << c; hence, the term “slow light.”
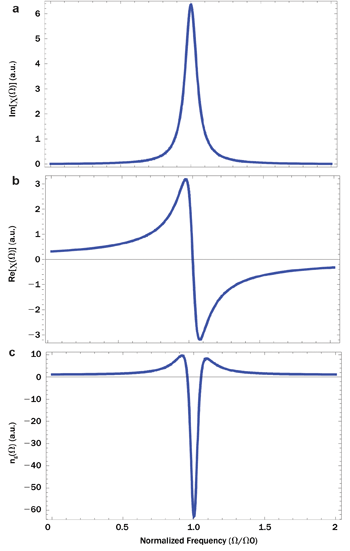
Figure 1. Kramers-Kronig theory relates the (a) absorption coefficients, (b) refractive and (c) group indices as functions of frequency. Photo courtesy of the authors.
For many applications, including telecommunications and sensing, very large and narrow absorption features produce the conditions leading to an extremely low group velocity. The most common figure of merit for defining the overall performance of a slow-light medium is the group delay bandwidth product (GBP), which emphasizes the fundamental trade-off between the amount of “slowing” and dynamic range. For example, in a telecommunications system, the GBP is the pulse delay divided by the pulse width or, for sensing applications, the bandwidth over which a reliable measurement can be performed, divided by the resolution.3 However, the amount of high-order dispersion and absorption typically increases with strong slow-light effects, causing pulse distortion.
Benchtop slow-light systems are available commercially as kits with room-temperature atomic rubidium (Rb) as the index-changing material (Figure 2, top left and bottom: a setup developed by the authors). Light from a tunable narrowband diode laser is passed through an electro-optic modulator to provide 3.5-ns pulses operating at the edges of the D2 absorption lines in Rb.4 Experimental setup data shows the (a) absorption (blue, cell at 40 °C) and transmission (red, cell at 90 °C), (b) refractive index, and (c) group index.5 The shaded regions offer the best compromise between group velocity, dispersion and absorption. The near-resonant pulses then propagate through a gas cell of length Lcell = 8.5 cm. Fine-tuning of the laser frequency allows for precision control of the group index. We observed a maximum value of 30, creating group velocities as low as 0.03c, equivalent to maximum delays of 10 ns (or GBP ~3). This increases the effective path length Leff (= ngLcell) for a pulse propagating through the interaction region of the cell to more than 3 m. This means the optical delay is more than 30 times the physical path length.
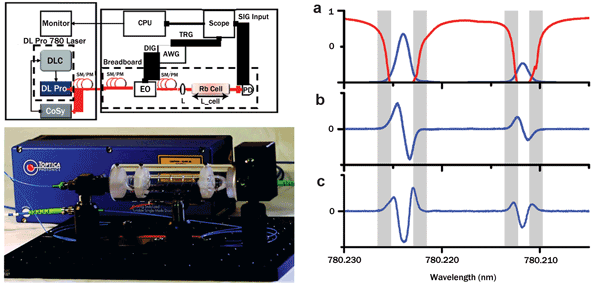
Figure 2. (Top left) Benchtop slow-light setup developed by the authors. (Bottom left) Experimental setup showing an 8.5-cm Rb cell and a tunable ultrastable laser source (Toptica Photonics DLC Pro 780). (Right) (a) Transmission (red) and absorption (blue) spectra, (b) refractive index spectrum, and (c) group index spectrum of the Rb cell. The gray regions indicate the preferred operating wavelengths. Photo courtesy of the authors.
The spectral sensitivity of this system can be controlled by varying system parameters such as temperature, rubidium density and density of any foreign gas within the cell, all of which influence the group index. In this setup, the cell is sealed and the temperature held constant. The group index is controlled by tuning the laser frequency. Therefore, source stability and precision are critical, including resistance to acoustic and temperature noise. As the data shows, this robust platform can be used for more ambitious experiments, such as the use of electromagnetically induced transparency (EIT) or high-Q resonators, which display sharper absorption features and hence much stronger slow-light effects.
Highly dispersive materials and structures
EIT has been used to slow down light to human speeds of 38 miles per hour.6 The resonant absorbing material was an ultracold gas of sodium cooled to nK temperatures, at the transition temperature to a Bose-Einstein condensate. Although EIT produces extreme group indices, most applications need the same strong dispersion but in conveniently available media such as bulk solid materials at room temperature or nanostructures.
Inspired by the results in the Bose-Einstein condensate, research has progressed toward more suitable media for real applications such as telecommunications. Experiments in crystalline solid ruby demonstrated slow light induced by the process of coherent population oscillation.7 However, broad background absorption limits the distance over which large group indices, and therefore low group velocities, can be achieved. Another approach is to use stimulated Brillouin scattering (SBS) in a room-temperature single-mode optical fiber.
This work is poised to be useful for optical data storage, optical buffering, optical delay and control units. The group indices induced by SBS are modest, typically <10, but are still interesting and useful, as the group delay can build up over long distances due to the low loss in modern optical fibers. SBS methods are being developed for the telecom market and other applications.
Industry’s demand for high-performance optical sensors and sources drove the race to engineer structures that are compatible with existing optoelectronics and that control and guide light. It is also useful to leverage semiconductor fabrication techniques. A few desired characteristics include tunable band curve and low cost, as well as robust, controlled strong dispersion leading to slow-light-enhancing effects.
More recently, focus has converged on PhCs as extremely promising and suitable structures to meet commercial demands. PhCs are defined as periodic dielectric optical structures with a refractive index modulation spacing that is on the wavelength scale of the incident light (typically a few hundred nanometers). Components can be tailored to operate in a broad wavelength range, including the visible and especially the telecom band at 1550 nm.
There are several useful configurations in 1-, 2- and 3-D.3 Currently the most common, weighing performance versus fabrication complexity, is a 2-D waveguide structure (Figure 3). Plotted is a theoretical calculation of the dispersion expected at the band edge of the transmission curve.8 The slow-light-enhanced operating region can be wavelength-selected and engineered to display strong dispersion, which is ideal for sensing.
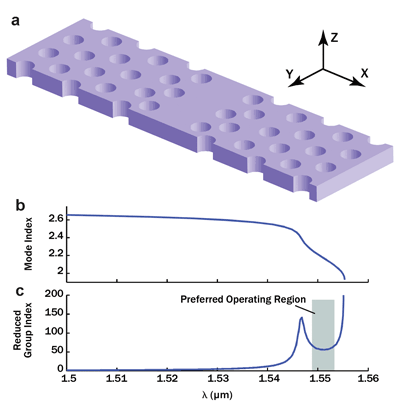
Figure 3. (a) An example of a 2-D PhC waveguide with line defects. Theoretical calculation of (b and c) dispersion near the band edge induces large slowing.8 Photo courtesy of Zhimin Shi.
Slow-light detection via interferometry
How is it possible to exploit the slow-light effect to precisely measure small observable features such as variations in refractive index, temperature or strain? Figure 4 shows a Fourier transform interferometer (a) in a standard configuration with one arm displaced with respect to one fixed arm, and (b) with tunable dispersive media (e.g., gas, PhC or both) placed in one of two arms. A photodiode at the end of the interferometer measures the phase difference between the two by changing the effective path difference in one arm. This is one of the most robust configurations for phase-to-amplitude conversion for sensing readout.
In the next few examples, we consider a slight variation to the Fourier transform that is shown, namely a Mach-Zehnder (MZ) interferometer. The spectral and sensor sensitivity of this slow-light-enhanced interferometer is proportional to the group index change of the medium.
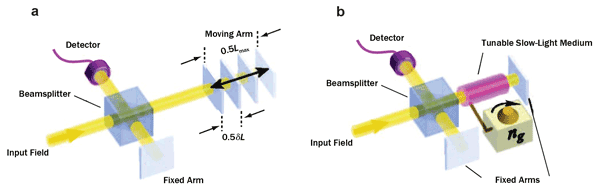
Figure 4. Interferometer examples with (a) one moving arm and one fixed, and (b) two fixed arms with a tunable dispersive medium inserted into one arm.4 Photo courtesy of American Physical Society.
Refractive index sensing can detect strain, stress, temperature fluctuation, molecular and atomic binding, and resonant absorption, and it continues to be developed for other applications. Bandgap devices such as fiber Bragg gratings (FBGs) for sensing are already used in the field to measure mechanical perturbations. Schemes for absorption sensing with PhCs for chemical and biological agents are being researched and developed. The interferometer configuration is a reliable tool for extracting physical measurements and is used ubiquitously for both.
Enhanced FBGs for perturbation sensing
Today, FBGs are commonly used in various industries including oil, gas, transportation, structural engineering and communications. Optical sensors provide several advantages over traditional electrical sensors: higher accuracy and performance, immunity to electromagnetic induction, easy installation, multiplexing and operation in fiber, and resistance to harsh mechanical environments.
As with Figure 4, we consider an MZ interferometer configuration with a transmission FBG in one arm, replacing the atomic cell in the other arm, operating at the band edge. Mechanical strain and temperature variations change the grating spacing, index and fiber mode, thereby shifting the Bragg wavelength, measured with the MZ as output fringe intensity shifts.
Figure 5 shows theoretical calculations of (a) the power transmission and (b) the group index plotted of a typical FBG. Preferred operation is at the edges of the band curve (the highlighted region), where very sharp features lead to large changes in the refractive index and hence strong sensing. The components are simple to construct, easily multiplexed and inexpensively fabricated directly into an optical fiber. Strain values using commercially based systems can be measured down to 10-10. However, in a slow-light-enhanced configuration, this value can reach as low as 8 × 10-13, which is ~700 times smaller than the lowest recorded from a non-slow-light-operating FBG.9 The measurement range for this illustration was limited to 11 pm.
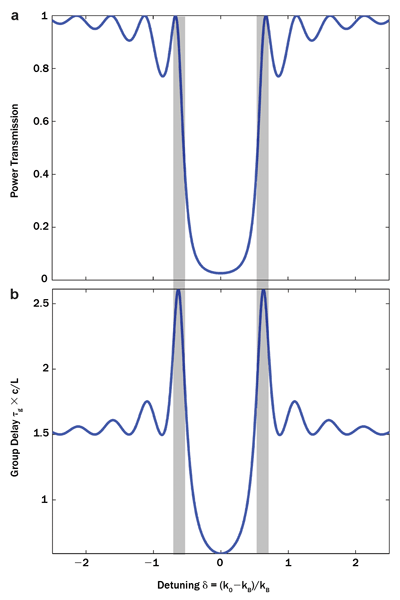
Figure 5. Typical simulated (a) power transmission and (b) group index spectrum of an FBG with preferred operating region highlighted in gray. Photo courtesy of the authors.
Highly sensitive absorption spectroscopy
Medical and defense applications embrace ideas proposing transportable, rugged devices with a small footprint for real-time detection in the field, where the need for improved performance is at the highest level. Engineered slow-light media can enable high sensitivity and spectral resolution for miniaturized devices. Simple scaling arguments show that the device can be made smaller by a factor as large as the group index while maintaining the spectral sensitivity of larger devices. This feature has the potential to advance many optical concepts and technologies.
Spectrometers are commonly used in many areas of fundamental research, as well as in applications including security and health care, to identify spectral fingerprints of molecular and biological agents.10 For such applications, a long path length is desirable, because the increased light-matter interaction results in a more sensitive detection of weak concentrations of gases and liquids. This is conventionally achieved by making multiple passes with a laser beam through the sample. However, this method only provides a limited enhancement in sensitivity. Furthermore, the increased volume of this setup limits efficiency, mobility and performance, and also restricts this unit to the laboratory.
Many optical designs use multi-pass optics to increase the actual optical path length through a small, constant sample volume. Multidimensional PhC structures such as 2-D waveguides offer a simple solution, allowing long effective-path distances of the physical structure for stronger absorption when operated in slow-light region. In addition, they can store liquids and gases, like traditional cells, in nanosize cells.11 The optical path through the gas is stretched by a factor proportional to the index change.
As with the FBG sensing example, by using an interferometer, the concentration can be detected with precision and within a small volume. This device could replace multi-pass cells and other bulky equipment in the laboratory with scalable and inexpensive units, without compromising performance.
Meet the authors
Dr. Michael E. Holmes is director of scientific laser sales at Toptica Photonics Inc. in Victor, N.Y.; email: [email protected]. Mohammad Mirhosseini is a graduate student in the Institute of Optics at the University of Rochester in New York state; email: [email protected]. Dr. Robert Boyd is Canada Excellence Research Chair at the University of Ottawa and also professor of optics and physics at the University of Rochester; email: [email protected].
Acknowledgments
The authors would like to thank Drs. Jerry Kuper and Chris Haimberger of Toptica Photonics for their valuable conversations and contributions. They also are grateful for the collaboration with professor Boyd’s group at the University of Rochester.
References
1. P.W. Milonni (2005). Slow Light, Fast Light, and Left-Handed Light. Institute of Physics Publishing.
2. J.B. Khurgin and R.S. Tucker, eds. (2008). Slow Light, Science and Applications. CRC Press.
3. R.W. Boyd and D.J. Gauthier (Nov. 20, 2009). Controlling the velocity of light pulses. Science, Vol. 326, pp. 1074-1077.
4. Z. Shi et al (Dec. 10, 2007). Slow-light Fourier transform interferometer. Phys Rev Lett, Vol. 99, 240801.
5. W. Ji et al (March 2007). Slow light propagation in a linear-response three-level atomic vapor. J Opt Soc Am B, Vol. 24, pp. 629-635.
6. L.V. Hau et al (Feb. 18, 1999). Light speed reduction to 17 metres per second in an ultracold atomic gas. Nature, Vol. 397, pp. 594-598.
7. M.S. Bigelow et al (July 11, 2003). Superluminal and slow light propagation in a room-temperature solid. Science, Vol. 301, pp. 200-202.
8. R.W. Boyd (Dec. 1, 2011). Material slow light and structural slow light. J Opt Soc Am B, Vol. 28, pp. A38-A44.
9. H. Wen et al (January 2012). Sensing with slow light in fiber Bragg gratings. IEEE Sens J, Vol. 12, p. 156.
10. A. Liapis et al (April 22, 2013). Optimizing photonic crystal waveguides for on-chip spectroscopic applications. Optics Express, Vol. 21, pp. 10160-10165.
11. Q. Wang et al (August 2013). Novel fiber optical gas sensor based on photonic crystal slow-light waveguide. Microwave Opt Technol Lett, Vol. 55, pp. 1796-1800.