Designing an optical system involves more than simply understanding the theory behind optics. To design a system efficiently and economically, it is important to understand the capabilities of an optical shop and the interaction of the specifications involved in ordering and designing components.
Warren J. Smith, Rockwell Collins Optronics
To the novice or casual user of optics, the acquisition of an optical system can be a very difficult experience. Failure to understand the ground rules can result in unnecessarily high cost, late delivery or impossibility of execution.
The best method for avoiding these problems is an early consultation with an optics vendor or designer. A wide range of experts is available: those who only design; those who design and furnish prototypes; and large organizations that can design, furnish and mass-produce the final system.
Optics is not like electronics. There are no breadboards that can be fixed in a few minutes with a soldering iron if the frequency response isn’t up to specifications. Once a lens is designed and built correctly, there is only an infinitesimal chance that tinkering with it will improve its performance significantly. An optical system often can be mocked up using stock components — which were probably designed for another type of application entirely — but if a high level of performance is needed, a system specifically tailored for the application usually is necessary.
Extreme care should be taken to specify only what is necessary and to allow the vendor/designer as much freedom as possible to balance and compromise in achieving the desired ends. When possible, specify only what can be tested — but bear in mind that an indirect test of a characteristic is often as good as a direct test. Be sure that the characteristic’s given tolerances are those that actually do affect the functional performance of your system.
A problem for all
One of the most difficult areas of optical engineering for both novice and expert is determination of the tolerances to be applied to specifications that are sent to the shop. On one hand, an overly generous set of allowances may lead to the failure of a well-designed system; on the other hand, tolerances that are too severe waste time and money for all concerned. In optics, this situation is further complicated by two factors: the tremendous range of tolerance sizes (e.g., from surface-regularity tolerances in tens of nanometers or microinches, to thickness variations in millimeters or hundredths of an inch); and the fact that, if enough time and money are available, almost any conceivable degree of accuracy is attainable.
The following must be borne in mind: First, every characteristic and dimension should be specified; the wide range of tolerance values indicates why box tolerances are almost never used in optics. Second, the tolerances should be geared to the capabilities of the shop; dimensions that are difficult for the shop to hold should be specified loosely. Third, you should look for ways in which the effect of a dimensional variation can be minimized; for example, the effect of a thickness variation may be vastly different, depending upon which surface of the element the mounting design fixes with respect to the balance of the system, and which surface is allowed to float. Some of the most frequently specified typical tolerances for these are summarized in Table 1. A table of this sort is of value chiefly for the newcomer to the strange and wonderful world of optical fabrication. Its function is primarily one of orientation, and it serves to give some feeling for what is readily feasible.
TABLE 1.
TYPICAL OPTICAL FABRICATION TOLERANCES
| |
|
|
Surface
Quality |
|
Diameter
(mm) |
|
Deviation
(Concentricity)
(min) |
|
Thickness
(mm) |
|
Radius |
|
Regularity
(Asphericity) |
|
Linear
Dimension
(mm) |
|
Angles |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Low Cost |
|
120 - 80 |
|
±0.20 |
|
>10 |
|
±0.50 |
|
Gauge |
|
Gauge |
|
±0.50 |
|
Degrees |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Commercial |
|
80 - 50
|
|
±0.07 |
|
3 - 0
|
|
±0.25 |
|
10 Fr
|
|
3 Fr
|
|
±0.25 |
|
±15' |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Precision |
|
60 - 40
|
|
±0.02 |
|
1 - 3
|
|
±0.10 |
|
5 Fr
|
|
1 Fr
|
|
±0.10 |
|
±5 - 10' |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Extra Precise
|
|
60 - 40
|
|
±0.01 |
|
<1 |
|
±0.05 |
|
1 Fr
|
|
1/5 Fr
|
|
As req'd.
|
|
Seconds |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Plastic |
|
80 - 50
|
|
±0.01 |
|
1 |
|
±0.02 |
|
10 Fr
|
|
5 Fr
|
|
0.02 |
|
Minutes |
The term quality used in reference to an optical surface is an indication of the finish of the surface (as opposed to accuracy, which describes the dimensional characteristics of the surface). Scratches, pits and chips on the surface, as well as bubbles, flaws and inclusions within the element, are defined by the quality specification. In the range of defect sizes usually permitted for precision optics, these are almost purely beauty defects and have little effect on the function of the system because the amount of energy they intercept is negligible.
The customary specification for surface defects is a two-number code. Originally, the first number specified the apparent width of the maximum size scratch in microns (it now is the scratch width in tenths of microns); the second number is the diameter, in hundredths of a millimeter, of the maximum size dig or pit. Inspection is by visual comparison with a set of graded standards. Further details of this system are given in MIL-O-13830.
A surface quality of 100-60 or 80-50 is adequate for most work. Smaller diameter elements or more critical applications may require a quality of 60-40 or 40-20, which will raise the production cost somewhat. Reticles and critical surfaces may require 20-10 or 10-5 surfaces. Such specifications should be called for only when absolutely necessary because of the greatly increased cost of producing such a clean surface.
High-power laser optics, on the other hand, may require extremely defect-free surfaces. Dirt, or a pit, may become a damage center and eventually destroy the optical element.
Surface accuracy
The term accuracy refers to the dimensional accuracy of the surface. In the case of a spherical surface, one specifies (1) a power tolerance; i.e., how far the mean radius of the surface may depart from the specified value, and (2) a regularity tolerance; i.e., how far the surface may depart from true sphericity. The specification usually is given in terms of the wavelength of the sodium D line, which is 589.3 nm. Inspection is accomplished by interferometric comparison with a master test plate and by observing the interference fringes (Newton’s rings) formed between the surface and the test gauge. The 632.8-nm wavelength of the HeNe laser also is frequently specified. The air space between the two surfaces changes one-half wavelength for each fringe.
The effects of the power tolerance, when expressed in fringes (i.e., when the tolerance is small), are usually small. When it is necessary to tolerance the radius, the tolerance should be based on a uniform increment of surface curvature (reciprocal radius), not radius. This produces radius tolerances that are proportional to the square of the radius. For example, the effect of a radius tolerance of 0.001 in. on a 1-in. radius is roughly equivalent to the effect of a 10-in. tolerance on a 100-in. radius:
C = 1/1 = 1.0 ± 0.001
vs.
C = 1/100 = 0.01 ± 0.001
The regularity tolerance can be evaluated on the basis of the Rayleigh λ/4 limit. An irregularity of one fringe introduces an optical path difference of (N’–N)/2 wavelengths, where N and N’ are the refractive indices on either side of the surface. For the total optical path difference to be less than one-quarter wavelength, the sum
n
∑ Fj (N'j — Nj)
j = 1
(where Fj is the number of fringes of irregularity at the jth surface) must be less than 0.5.
Power tolerances
Tolerances of 5 to 10 fringes power variation and 1/2 to 1 fringe irregularity are quite common. Power tolerances of 1 to 3 fringes, with correspondingly improved regularity, can be obtained with a corresponding increase in cost. It is important to note that these are shop tolerances with respect to a specific test plate, and that it is advisable to determine what radii are available in the vendor’s shop as stock tooling before specifying surface power in this manner. Frequently, the surfaces are not given power tolerances at all; the focal lengths and/or the system performance are toleranced instead. The changes in radius and curvature corresponding to N fringes over a diameter D for a wavelength are given by:
ΔR = 4NλR2/D2
ΔC = 4Nλ/D2
Surprisingly, thickness tolerances are among the most difficult for a production optical shop to hold. Unfortunately, they are among the more important tolerances in many systems. Those systems in which the ray slope angles are large usually are demanding in this regard. Meniscus (double Gauss) anastigmats and high-aperture microscope objectives are typical examples of systems where thickness is critical.
For ordinary precision work, ±0.1 mm is a typical thickness tolerance, although ±0.15 or ±0.20 is more economical. If extreme care is taken, a tolerance of ±0.05 mm can be held in production, but the cost is high unless production runs are large enough to justify special tooling such as spot blockers.
Centering
Centering tolerances are twofold. The diameter of an element can readily be held to a tolerance of +0.00, –0.03 mm. The accuracy with which the optical axis is aligned to the mechanical axis usually is specified in terms of angular deviation — the deviation of an axial ray directed toward the mechanical center of the element (Figure 1). This is convenient because the total deviation of a system is the (vector) sum of the individual deviations of the elements. On mechanical cone centering machines, the deviation will be about 1/D min of arc, where D is the element diameter in inches.
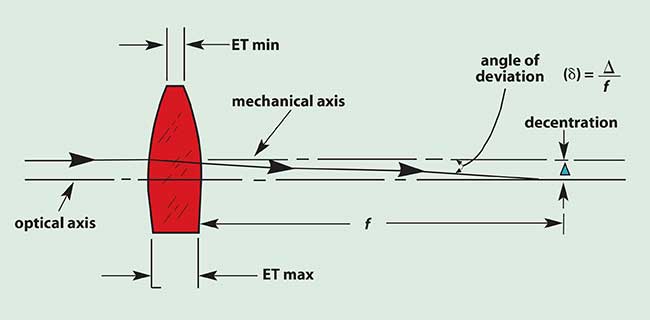
Figure 1. Illustration of the relationship between the optical and mechanical axes, and the decentration and angle of deviation in a decentered lens.
Visual centering is capable of much better accuracy; for example, 0.1 min can be achieved for long radii. In such cases, the accuracy is a function of the radius and magnification used; 1 or 2 min is a typical tolerance.
Note that a decentered element can be considered as a centered element plus a thin deviating wedge. When elements are fabricated without a separate centering operation (for reasons of economy), diameters can be held to ±0.05 or ±0.1 mm and the wedge (across the diameter) to 0.1 to 0.2 mm. The deviation of a thin wedge is (N – 1) × angle.
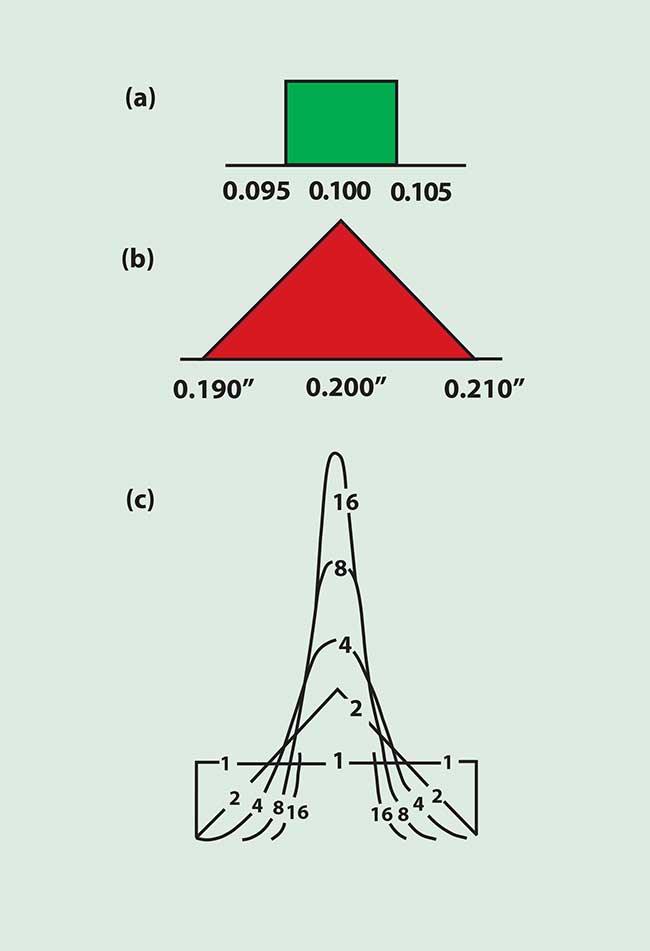
Figure 2. Illustration of the manner in which
additive tolerances combine in assembly. Plot (a) shows a uniform
probability in a dimension of a single piece. When two such pieces are
combined, the frequency distribution is shown in (b). Normalized curves
for assemblies of 1, 2, 4, 8 and 16 pieces are shown in (c).
Prism linear dimensions, like thicknesses, are hard for the optical shop to control. One should try to tolerance only dimensions that can be measured — that is, not dimensions to sharp corners that have been beveled. Tolerances of 0.1 to 0.2 mm are typical.
Statistical tolerancing
Consider a stack of discs, each 0.1-in. thick and made to a tolerance of ±0.005, and assume that there is an even chance that the thickness of a disc will fall at any given value within this tolerance. Thus, there is one chance in 10 that the thickness of a disc will lie between 0.095 and 0.096 in. When two discs are combined, the probability that their total thickness is between 0.190 and 0.192 in. is one-tenth of one-tenth, or one in 100 (Figure 2).
The above gives some insight into the commonly used rule of thumb for tolerancing, which is:
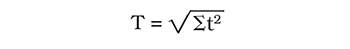and states that the probable total effect, T, of a set of additive tolerances is equal to the square root of the sum of the squares (rss) of the individual tolerance effects. The central limit theorem says that the more variables we have, the more the distribution peaks at about its central values. If t represents the tolerance range for x percent (say 99 percent) of the parts, then T will be the range for x percent (say 99 percent) of the assemblies.
A statistical approach to optical tolerancing is eminently justifiable. Consider a simple air-spaced triplet (Cooke-Taylor) anastigmat. With six curvatures, three thicknesses, two air spaces and three indices, there are no fewer than 14 tolerances that additively affect the monochromatic aberrations and focal lengths of the system. Note that this treatment does not depend on the quantity of assemblies produced; it depends only on the quantity of pieces/tolerances that go into the assembly.
The tolerance set or budget for an optical system usually is worked out as the last step in the lens-design process. The designer calculates the change in the various aberrations that are produced by small (tolerance size) changes in the system’s dimensions. Often a table of the sort presented in Table 1 is used to select an initial trial tolerance budget. The effect of the trial budget on the system performance can be evaluated by assuming that the individual tolerance-induced effects will combine randomly with each other and with the inherent aberrations of the nominal design. This can be handled easily by adopting the wavefront deformation or optical path difference as a common metric for all the aberrations and combining them according to the rss given above. The use of optical path difference as the metric makes it easy to evaluate the effect of the tolerance-induced aberrations on the system performance.
Human nature being what it is, the initial selection of the tolerance budget is often optimistic and thus requires adjustment. Some dimensions are very sensitive; some are not. The tolerance budgeteer will likely want to tighten the tolerances on the sensitive parameters and loosen the insensitive ones. But there are limits on this process, and this is where a modest knowledge of the capabilities of the optical shop can be worthwile.
Probably every optical shop has what might be called a tolerance profile. The opticians, the equipment, the techniques and the test procedures are all set up to maintain a certain level of tolerances. If you specify looser tolerances — twice as large, for example — you may benefit from a small savings because the rejection rate (which is probably already quite small for the shop’s normal tolerances) will be reduced. Double the tolerances again, and the cost will hardly budge because the shop is not going to change its procedures to make bad parts just for you. Thus it is apparent that there is a tolerance level beyond which there are no savings to be achieved.
Conversely, if tolerances are tightened beyond the shop’s normal levels, costs immediately begin to rise (as will the cries of pain from your supplier). If you reduce tolerances enough, at some point your specification may prove to be impossible for the shop to meet. As this point is approached, the expense climbs toward infinity.
References
Deve, C. (1954). Optical Workshop Principles. Hilger & Watts, London.
Horne, D.F. (1972). Optical Production Technology. Crane Russak & Co., New York.
McLeod and Sherwood (1945). A proposed method of specifying appearance defects of optical
parts. J. OPT. SOC. AMER. 35: 136-138.
MIL-Hbk 141 (1962). Optical Design. Department of Defense, Washington. MIL-0-13830,
“Optical Components for Fire Control Instruments.”
Smith, Warren J. (2000). Modern Optical Engineering. 3rd. Ed. McGraw-Hill, New York.
Twyman (1952). Prism and Lens Making. Hilger & Watts, London.