By: Dr. Stephen D. Fantone, Dr. David Imrie and Dr. Jian Zhang
With cameras being used in applications ranging from consumer products such as PDAs, automotive rear viewing systems, and medical devices to military applications including thermal imaging and ranging systems, how does one rationally compare the performance of these cameras?
No single metric can fully describe the performance of an imager and no short article can thoroughly treat the complexities of testing the performance of an imaging camera. Instead, this article is intended to describe some of the more important evaluation metrics that are used to assess overall camera performance.
One of the reasons that the application areas for imaging have exploded is that camera technologies themselves are changing. It is helpful to divide cameras into those that rely on reflected light (visible, near, and short wave infrared, 350 nm – 2.5 microns wavelength) and those that rely on imaging the thermal emissions of the object itself (3-14 microns wavelength). Cameras working in the visible and near infrared use silicon based devices, near short wave infrared-red cameras use InGaAs, and thermal infrared imagers (both cooled and uncooled) use MCT and InSb.
The past few years have seen the widespread adoption of a number of digital high speed serial camera output formats: USB 2.0, IEEE-1394 (“FireWire”), CameraLink, and gigabit Ethernet (“GigE”), greatly expanding the transmission and interfacing of video signals. At the same time proprietary parallel digital camera LVDS outputs (parallel data is particularly well suited to non-standard formats and line scan cameras) and standard analog video remain popular. With camera manufacturers adhering to standard data formats (such as the DCAM standard for FireWire) to varying extents, the challenge for camera test equipment is to seamlessly interface with all of these formats.
How can I verify my camera’s performance? Is comparing the resolutions (number of pixels) and responsivities of two cameras sufficient to make an appropriate choice? What do I need to measure at incoming inspection to make sure my cameras will perform as they should?
Listed below is a sampling of camera performance metrics:
• Pixel size (the actual area that is sensitive to light)
• Cell size (the spacing of pixels in the imager)
• Number of pixels (horizontal and vertical)
• Signal Transfer Function (SiTF), Modulation Transfer Function (MTF)
• Responsivity and Linearity
• Noise
• Spectral sensitivity
Optikos Corporation has long been a major provider of software and test hardware that allows the user to objectively assess the performance of imagers of all types by making measurements of, for example, the Signal Transfer Function, Modulation Transfer Function, linearity, and noise characteristics of cameras.
Its I-SITE (Imaging-Systems Integrated Test Equipment) software has evolved with the development of new camera types to allow full characterization of camera performance across the spectrum with a particular emphasis on measuring the performance of thermal imaging systems.
Although the I-SITE software package is capable of evaluating any type of camera, the test hardware with which it is integrated is tailored to meet the requirements of the particular waveband of interest. In the visible and near infrared, test targets are illuminated with extended sources in which the absolute luminance or visible contrast can be precisely controlled, whereas in the thermal infrared it is the radiometric temperature difference between the foreground and background in a target that is held constant in a thermal test target generator.
Some parameters such as pixel count, pixel and cell size are so tightly controlled in the fabrication process that they do not need to be directly measured by the end user, but can be confidently relied on from specification sheets. And while pixel count and size are important measures of system performance, in part because they set upper bounds for the potential resolution in a system, they do not by themselves ensure adequate resolution or imaging. Many other factors come into play including sensitivity, spectral response, noise, and, of course, the optics that are used in conjunction with the camera.
The relative dimensions of the pixel size and the cell size provide information regarding the relative efficiency of the imager in actually having light that is incident on the imager reach a photo responsive area. This efficiency can be increased by placing lenslet arrays on top of the imager, effectively making the apparent size of each pixel appear to be a larger percentage of the cell size.
It is useful to apply linear system theory to understand and describe camera performance, but it needs to be understood that pixelated camera systems violate one of the principles of linear system theory, that of shift invariance. This can be understood by noting that if a sub-pixel spot is imaged onto a camera sensor within a single pixel, a slight displacement of the spot does not result in a shift in the representation of the spot that is output from the camera. Thus, the spatial phasing of an image relative to individual pixels can significantly affect the signal output.
Another example is the imaging of a periodic structure like a picket fence onto an imager containing a regular array of pixels. The output of the camera can fully resolve the picket fence when the fence slats are directly aligned with individual columns of pixels, but if the fence slats span the boundary of two pixels then the picket fence will not be resolved. Further complicating this phasing effect are mismatches in the periodic frequency and alignment between objects and pixel arrays, giving rise to the aliasing effects and moiré patterns that are frequently observed in pixelated imaging systems. It is beyond the scope of this article to describe the approaches to mitigating these effects, but they can be reduced to acceptable levels with careful control of the F/# and imaging performance of the lens and the use of anti-aliasing filters. When measuring a spatial resolution metric of a pixelated camera, such as its MTF, it is important to do so in a manner that yields a result that is independent of the effects described above.
It is natural to think that a camera should operate as a linear device and that the output of a camera should be a linear scaling of the luminance of the object it is imaging. This is the case with instrumentation cameras which act as linear photometers or radiometers. In these cases it is important that the signal output from the camera be in strict proportion to the light input. For conventional photographic imaging, this is not the case, and some compression or expansion of the dynamic range of a camera is desirable. For instance, in an 8 bit imaging system, the range of brightness is normally 256:1. In a photographic application, a linear representation of luminance would not provide a satisfactory image since detail in the high brightness areas would be lost. In traditional photographic emulsions, the range is extended by having a non-linear response so that there is extended response in both the highlights and shadows.
Camera testing is different from system testing because of the need to separately account for the limitations of the lens. In many camera systems, the system MTF is dominated by the lens MTF. In camera testing, it is important to ensure that the contribution of the lens to the degradation in MTF is relatively small and can be taken into account. Depending on the application, there are different approaches to separating out the effect of lens performance. In the thermal infrared, a good quality low f/# lens will work since the diffraction spot size is approximately 10x larger than in a visible lens. For visible and UV cameras, the pixel size is usually on the order of a few microns and a high performance lens is usually necessary to form a low F/# diffraction limited image on the camera sensor.
Sampling in camera testing is a special challenge. In lens testing, the aerial image may be well sampled by employing a magnifying relay or scanning the image plane with a slit or knife edge at high spatial resolution in the case of IR lens testing. In camera testing, the simplest approach is the “sloping slit” technique. In this case, a slit is imaged onto the array of pixels. Consider the problem of measuring the horizontal resolution of a thermal imager. Sub-pixel sampling of the line spread function of a slit target is achieved using successive lines in the image to shift the phase of the sample bins by less than one pixel. The line spread function can then be reconstructed mathematically using multiple lines, and from the line spread function the MTF may be obtained.
Another approach is to scan the line across the pixels in sub-pixel steps and to reconstruct the line spread function from the rows of pixels captured at each scan position. Because multiple rows may be averaged, the signal to noise ratio using this technique is superior to that of the sloping slit approach. Furthermore, sub-pixel scanning can be very precisely achieved by scanning the target in linear space at the focus of a collimator. The demagnification ratio of the lens permits fine scanning at the camera sensor. Figure 1 shows the line spread function and corresponding MTF measured in this manner.
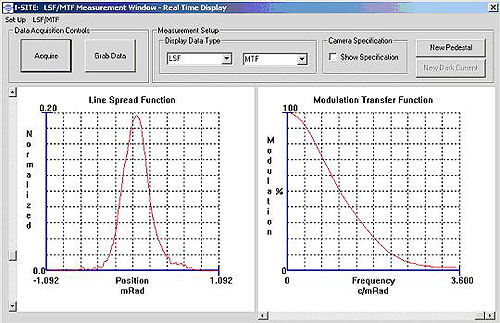
Figure 1: Modular Transfer Function (MTF) test module. I-SITE implements the source scanning methods and the sloping slit method to oversample the Line Spread Function (LSF) displayed at left.
High sensitivity alone does not ensure good imagery. A camera with high background noise can easily overpower any benefit from a high sensitivity imager. Clearly, both sensitivity and noise need to be evaluated simultaneously. One way of doing this is to measure the Signal Transfer Function, as seen in Figure 2, which, in the case of Thermal Imagers may be used to calculate the Noise Equivalent Temperature Difference (NETD), one of the most important thermal camera performance metrics.
Additional information regarding the power distribution of the noise in the image in spatial frequency space may be found by extracting the Noise Power Spectrum from the video signal. A snapshot of one such spectrum is shown in Figure 3.
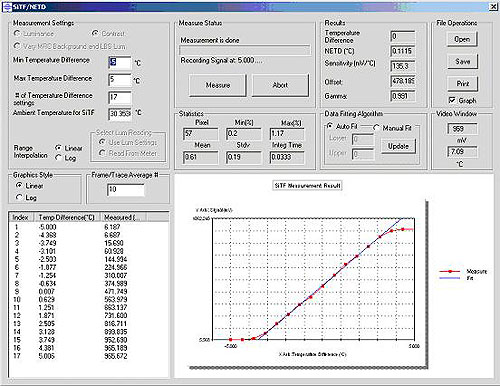
Figure 2. I-SITE Signal Transfer Function (SiTF) measurement module. Within the characteristic S-shape of the SiTF curve, the software has automatically located the linear response region and performed a least-squares straight line fit. The sensitivity and NETD of the thermal imager are calculated from the fitting.
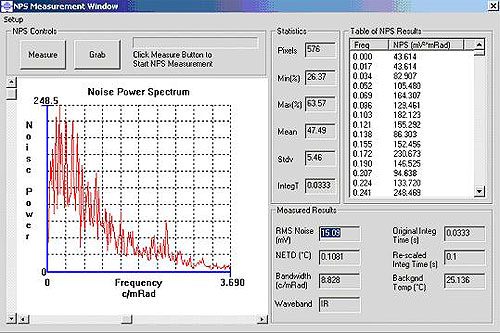
Figure 3: The Noise Power Spectrum (NPS) test module. The chart displays the noise power density as a function of the spatial frequency, showing characteristic noise spikes at certain spatial frequencies. In this example, the cutoff frequency of the low pass filter utilized in the thermal imager can be seen. Both root mean square noise (RMS Noise) and noise equivalent temperature difference (NETD) are calculated and displayed.
Another important measure of a thermal camera system is its Minimum Resolvable Temperature Difference (MRTD). As one might expect, the spatial frequency of the smallest target that can be resolved in a thermal camera increases as the temperature difference between the background and foreground drops. For this reason, the MRTD of a thermal camera is not a single number but a graph of MRTD vs spatial frequency. The techniques for measuring MRTD are varied and nuanced enough to warrant their own article. Both objective and subjective methods are employed, and in the case of the objective methods a calibration function is required in order to standardize the results. This calibration factor may be obtained by using trained human observers or by applying a standard eye model as is shown in the case illustrated in Figure 4.
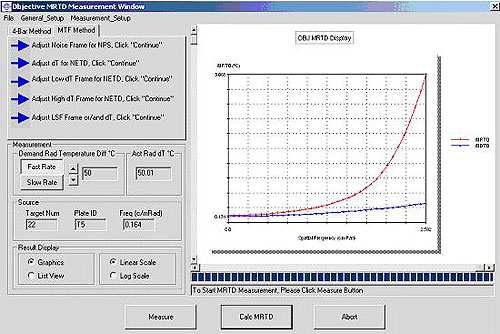
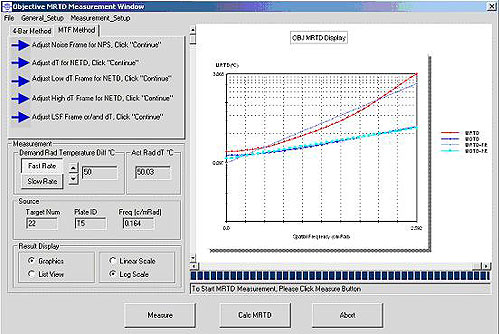
Figure 4-5: Objective Minimum Resolvable Temperature Difference (MRTD) and Minimum Detectable Temperature Difference (MDTD) test module. I-SITE sequentially measures the NPS, SiTF, NETD and MTF of the thermal imager then calculates the MRTD/MDTD for multiple spatial frequencies using a standard human eye model.
No longer of importance solely to government laboratories and defense contractors, the objective evaluation of imaging cameras has become a competitive concern for the manufacturers of quality consumer goods and medical devices. Specialized software and equipment for testing cameras is playing an essential role in both the incoming inspection and product qualification departments of a wide range of camera-based equipment manufacturers. Increasingly, the sequencing of tests is becoming highly automated so batteries of tests once undertaken by a skilled engineer may now be undertaken by a technician in a significantly shorter timeframe.
Meet the authors...
Stephen D. Fantone, Ph.D., is the founder, chief executive officer and president of Optikos Corp. in Wakefield, MA.; e-mail: [email protected]
David Imrie, Ph.D., serves as the chief technology officer and VP of Core Technology at Optikos; email: [email protected]
Jian Zhang, Ph.D., serves as the software engineering manager and as an engineering fellow at Optikos; email: [email protected]
Optikos Corporation is an optical engineering firm specializing in optical instrumentation, test equipment, industrial and medical systems, and consumer products. For more information, visit: www.optikos.com
Also see: More Web Exclusives