How can the speed of light be reduced a millionfold, and why does this matter? The answers to these questions are intriguing and important.
Daniel J. Gauthier, Duke University, Alexander L. Gaeta, Cornell University, and Robert W. Boyd, University of Rochester
The speed of light in a vacuum is a quantity that defies human comprehension. A flash of light travels across a football field so quickly that it appears instantaneous; it is only through the use of modern high-speed photoreceivers that we can measure the propagation time delay. But now, in several laboratories around the world, light speed is approaching the human scale.
Recent research from the nonlinear and quantum optics communities has demonstrated exquisite control over the speed of a pulse of light as it propagates through a material system.1 It is possible to control the speed of a pulse of light from its vacuum speed — 3 × 108 m/s — all the way down to the speed of a good bicyclist — a few meters per second. In part, such efforts have been motivated by the need for optically controllable pulse delays for applications such as optical buffering, data synchronization, optical memory and signal processing (see “Toward Optical Packet Switching,” page 84).
This article offers background on such slow-light investigations and summarizes some recent demonstrations that employed components that could be integrated into real-world systems — for example, into a telecommunications network.
To understand these results, it is crucial to realize that many velocities characterize how a pulse propagates through an optical medium.2 This confusing situation arises from the fact that a pulse propagating through any material system experiences some level of distortion (e.g., it spreads out in time and is reshaped) and, hence, cannot be assigned a single velocity.
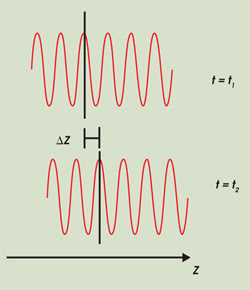
Figure 1. Snapshots of the electric field of a monochromatic electromagnetic wave are shown at two times as the wave propagates through an optical material. The phase velocity describes the speed of the crests of the wave. The distance traveled by a crest in the time interval t2 to t1 is denoted by Δz.
Probably the most familiar is the phase velocity of light. Consider a continuous-wave monochromatic (single frequency) beam of light of frequency ωc. The electromagnetic field oscillates rapidly; for example, the oscillation period is approximately 1.8 fs for green light. The phase velocity describes the speed at which the crest of these oscillations propagates (Figure 1). In a material system, characterized by the frequency-dependent index of refractions n(ω), the phase velocity vp is defined as
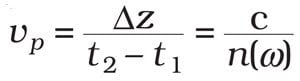where Δz denotes the distance traveled by a crest in the time interval t2 to t1 and c is the speed of light in a vacuum.
The situation becomes more complicated when a pulse of light propagates through a dispersive optical medium. Via Fourier’s theorem, a pulse of duration t comprises a range of frequencies. In a sense, a pulse can be thought of as resulting from constructive and destructive interference among various Fourier (frequency) components. At the peak of the pulse, the components tend to add up in phase and to interfere destructively in the temporal wings of the pulse (Figure 2).
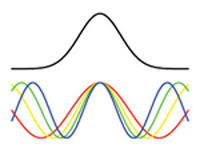
Figure 2. Sinusoidal component waves interfere to create a pulse of light.
In a material with a refractive index that is frequency-dependent, each of these frequencies propagates with a different phase velocity, thereby disrupting the interference. If n(ω) varies linearly as a function of ω, the effect of the disrupted interference is to temporally shift the pulse with respect to the same pulse traveling through vacuum, but the pulse shape stays the same. The fact that the pulse is temporally shifted implies that it is traveling at a different velocity — known as the group velocity vg, which is defined as
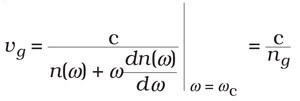where ωc is the central frequency and ng is the group index of the material. We see that ng differs from the phase index by a term that depends on the dispersion of the refractive index dn/dω.
Slow-light effects invariably make use of the rapid variation of refractive index that occurs in the vicinity of a material resonance. Slow light, in which vg << c, can be achieved by making dn/dω large and positive; i.e., a situation of large normal chromatic dispersion. What is perhaps most significant about the slow-light research is not the magnitude of the effect but rather the realization that pulses can propagate through highly dispersive media with negligible pulse distortion.
Higher-order dispersion, arising from the nonlinear dependence of n(ω) on ω, is responsible for distorting the shape of the pulse. The recent slow-light experiments have been conducted in a regime that minimizes higher-order dispersion. However, the pulse bandwidth has to be limited to the spectral region over which there is essentially a linear variation of n(ω).
This limit implies that the pulse duration cannot be too short. The slowest group velocities that have been observed in the laboratory have been obtained for pulses that are on the order of a few microseconds. One focus of current research is to develop methods of achieving slow light at higher bandwidths.
Resonant atomic systems
For achieving extremely slow light, it is important to find a material system in which dn/dω is as large (and positive) as possible. A dilute gas of atoms with a strong absorption resonance is an interesting candidate.
The refractive index for such a sample is typically small (n – 1 Å 10–3 ), but it varies rapidly in the region of the resonance so that dn/dω and, hence, ng can be large (Figure 3). As the carrier frequency of a pulse is tuned near the resonance frequency, the normal dispersion becomes very large. For easily attainable conditions, vg/c ≈ 10–6; i.e., vg ≈ 300 m/s. However, the absorption near a resonance is very high. Essentially, all of the light is absorbed in a few microns, severely limiting the attainable slow-light delay. (Note that the group index can take on values that are less than 1 or even that are negative, the significance of which is mentioned below.)
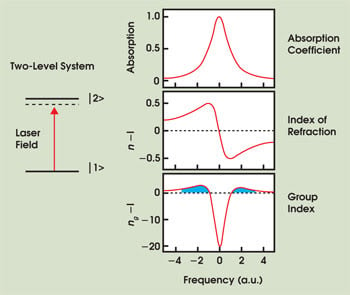
Figure 3. In a two-level system, the strong absorption resonance gives rise to a large variation in the refractive index and group index in the vicinity of the resonance. Slow light occurs on either side of the resonance where ng is large and positive, indicated by blue shading in the group-index plot. (The vertical scales of the two index plots are not the same.)
A revolution in the field came when Stephen E. Harris’ group at Stanford University in California realized that the slow-light effect can be preserved while the effects of absorption are simultaneously canceled using a coherent optical effect occurring in a gas of atoms that have three energy levels.3,4 The frequency of a strong auxiliary laser beam, often called the coupling laser, is tuned to one of the resonances (Figure 4). It causes a narrow dip in the absorption coefficient (a high-transmission window) and a process known as electromagnetically induced transparency. Associated with this transparency window is a rapid variation in the refractive index in the vicinity of the dip. This offers the best of both worlds: large normal dispersion and high transmission. Of course, the spectral extent of the pulse must fit within this narrow transparency window.
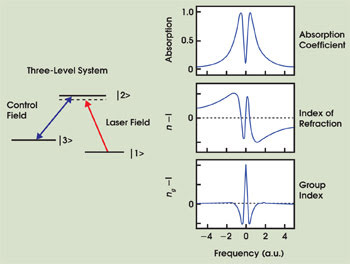
Figure 4. In a three-level system, the control field creates a narrow region of transparency at the center of the absorption line because of a quantum interference effect. Large normal chromatic dispersion occurs in the transparency window, giving rise to a large positive value ng at the center of the resonance.
The experimental slow-light results using electromagnetically induced transparency have been impressive. Using cold5 or warm6,7 gases of three-level atoms, group velocities as low as 8 m/s for 125-ms-long pulses have been observed (see “Physicists Bring Light to a Crawl,” Photonics Spectra, April 1999, page 26, and “Slow It Down,” September 1999, page 44).
These results have triggered a flurry of research on new methods for controlling the properties of light at the classical and quantum level using coherent optical methods. They also have motivated research on transitioning these results to much higher bandwidths — i.e., shorter pulses — that operate at the telecommunications band around 1.55 μm.
Another goal is to identify methods that do not require an atomic resonance, which limits the spectral regions where slow light can be achieved.
As impressive as these results are, slow light based on electromagnetically induced transparency typically requires that the material medium be a low-density atomic vapor or an impurity-doped solid maintained at low temperature.
Coherent population oscillations
The reason for these restrictions is that the electromagnetically induced transparency process involves delicate quantum interference between two quantum amplitudes, and the presence of collisions or other dephasing phenomena can destroy this interference. That process thus has not been observed in a room-temperature solid-state material, which would be desirable for practical uses of slow-light methods. However, the process of coherent population oscillations also leads to very slow propagation of light pulses, and this can occur in room-temperature solids.
When a strong pump beam and a signal beam of slightly different frequencies interact in a material that displays saturable absorption, the population of the ground state of the material will oscillate in time at the beat frequency of the two input waves. This effect is known as a coherent population oscillation. Because it involves populations, it is highly insensitive to dephasing processes. Mathematical analysis shows that the presence of coherent population oscillations produces a rapid frequency variation of the refractive index, which leads to a large value of the group index.
Slow light based on coherent population oscillations has been studied in a variety of material systems. Experiments performed in ruby in Robert W. Boyd’s laboratory at the University of Rochester in New York established that slow light based on this effect could be observed, and the team reported group indices as large as several million (see “Ruby Crystal Slows Light at Room Temperature,” Photonics Spectra, May 2003, page 97, and erratum, June 2003, page 12).8
An intriguing variant of this behavior has been observed in alexandrite (see “Investigations Probe Ultraslow and Superluminal Light,” September 2003, page 92). At certain wavelengths, alexandrite acts as an inverse saturable absorber: The absorption of the material increases with increasing optical intensity.
At these wavelengths, the induced change in the group index has the opposite sign than for a saturable absorber, and the group index consequently can be less than unity or even negative. This sort of superluminal propagation was demonstrated in the laboratory.9 Modification of the group velocity by coherent population oscillations also has been observed in erbium-doped optical materials10,11 and in semiconductor structures.12
As noted earlier, a key issue in all slow-light experiments is the maximum modulation bandwidth — roughly the inverse of the shortest pulse — that can experience the full slow-light effect. In coherent population oscillation experiments, this bandwidth is set by the inverse of the population recovery time t1. The early experiments based on ruby, alexandrite and erbium led to highly restricted bandwidths on the order of 1 kHz as a consequence of the long population relaxation times of these materials, implying that the materials can be used to delay pulses not much shorter than 1 ms.
More recent research has targeted the development of materials with a much faster population recovery. For instance, Xiaoxue Zhao and colleagues at the University of California, Berkeley, and Texas A&M University in College Station observed slow light with a modulation bandwidth as large as 2.8 GHz in a semiconductor laser amplifier, which can be used to delay pulses as short as 125 ps.
Stimulated scattering
Light scattering occurs as a result of highly localized changes in the dielectric constant of a medium. For sufficiently strong light fields, these changes can be induced via the coupling of a material excitation to two light fields whose difference in frequencies is given by the frequency of the excitation. This is known as stimulated scattering.
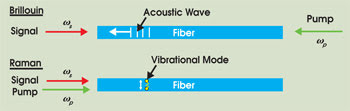
Figure 5. In the Brillouin process, light is scattered from the pump to the signal field via a propagating acoustic wave. In the Raman process, light is scattered from the pump to the signal field via vibrational modes of molecules in the fiber.
The two most commonly observed forms of stimulated scattering are stimulated Brillouin scattering and stimulated Raman scattering, in which a high-frequency acoustic wave and a vibrational excitation, respectively, are induced in the material. These processes transfer light energy from the higher-frequency light field (i.e., the pump or control field) to the lower-frequency one (i.e., the signal or data field), which results in the exponential amplification of the signal field when its frequency is detuned from the pump field by the excitation frequency (i.e., the acoustic frequency or the vibrational frequency).
The resulting gain occurs over a certain gain bandwidth and scales with the intensity of the pump field. This amplification process for the signal field also is accompanied by a spectrally varying refractive index, which gives rise to slow light that can be controlled simply by changing the power of the pump field.
Controllable slow-light delays due to stimulated Brillouin scattering in conventional telecommunication fibers have been realized independently by two teams. The first involved the efforts of Miguel González-Herráez of Universidad de Alcalá in Madrid, Spain, while on sabbatical leave at Ecole Polytechnique Fédérale de Lausanne in Switzerland with Luc Thèvenaz’s group.13 The second involved a collaboration of scientists — including the authors of this article — from Cornell University in Ithaca, N.Y., the University of Rochester and Duke University in Durham, N.C. (see “‘Slow Light’ Demonstrated in Optical Fiber,” July 2005, page 115).14
Neither team observed the very low group velocities achieved in atomic gases. However, it is the tunable delay relative to the duration of a pulse that is the critical metric for numerous applications, not the total reduction in the group velocity. Although the maximum delay in a single stage in these experiments was on the order of a pulse width, this is sufficient for telecommunication applications such as the optical retiming of an optical clock to data pulses.
Another issue in these stimulated Brillouin scattering experiments is that the bandwidth over which slow light could be generated was limited to less than 100 MHz. However, efforts by both groups have shown that the bandwidth can be pushed to frequencies beyond 1 GHz — and perhaps to telecommunications bandwidths of 10 GHz (supporting slow light for approximately 35-ps-long pulses).
Alternatively, the bandwidth associated with stimulated Raman scattering in fibers is large enough to support very high data rates. Alexander L. Gaeta’s group at Cornell achieved slow-light delay of a pulse width for subpicosecond pulses,15 paving the way for ultrahigh data rate networks operating near 1 Tb/s. Gadi Eisenstein’s group at Technion in Haifa, Israel, demonstrated slow light via the nonlinear optical process of Raman-assisted four-wave mixing.16
The use of stimulated scattering to produce tunable delays has a number of advantages over previously demonstrated slow-light techniques because “off the shelf” it can utilize telecommunications components, which reduces the overall cost and allows straightforward integration with the existing telecommunications infrastructure. In addition, by tuning the frequency of the pump wave, the slow-light resonance can be tuned to any wavelength within the S-, C- and L-band optical communications windows. Efforts are under way by several groups to increase the delays to nearly 1000 pulse widths, which will be needed for the typical data packets processed by today’s routers.
Future prospects
There has been very rapid progress in the past few years in improving the bandwidth of slow light and in transitioning the technology to telecommunications wavelengths using fairly standard off-the-shelf components. We believe that the most promising of these technologies will soon be found in high-speed telecommunication regenerators for resynchronizing the data stream with the clock and as true time delay devices for synthetic-aperture radar. Eventually, they may find their way into optical buffering applications, if enough total slow-light delay can be achieved with low pulse distortion.
Acknowledgment
The authors gratefully acknowledge the financial support of DARPA’s Defense Sciences Office through its slow-light program.
Meet the authors
Daniel J. Gauthier is Anne T. and Robert M. Bass professor of physics and biomedical engineering and chairman of the department of physics at Duke University in Durham, N.C.; e-mail: [email protected].
Alexander L. Gaeta is a professor in the School of Applied and Engineering Physics at Cornell University in Ithaca, N.Y.; e-mail: [email protected].
Robert W. Boyd is M. Parker Givens professor of optics at the Institute of Optics and a professor of physics at the University of Rochester in Rochester, N.Y.; e-mail: [email protected].
References
1. R.W. Boyd and D.J. Gauthier (2002). Progress in Optics, Vol. 43. Emil Wolf, ed. Elsevier, pp. 497-530.
2. R.L. Smith (August 1970). The velocities of light. AM J PHYS, pp. 978-984.
3. S.E. Harris, J.E. Field and A. Imamogùlu (March 5, 1990). Nonlinear optical processes using electromagnetically induced transparency. PHYS REV LETT, pp. 1107-1110.
4. S.E. Harris, J.E. Field and A. Kasapi (July 1, 1992). Dispersive properties of electromagnetically induced transparency. PHYS REV A, pp. R29-R32.
5. L.V. Hau et al (Feb. 18, 1999). Light speed reduction to 17 metres per second in an ultracold atomic gas. NATURE, pp. 594-598.
6. M.M. Kash et al (June 28, 1999). Ultraslow group velocity and enhanced nonlinear optical effects in a coherently driven hot atomic gas. PHYS REV LETT, pp. 5229-5232.
7. D. Budker et al (Aug. 30, 1999). Nonlinear magneto-optics and reduced group velocity of light in atomic vapor with slow ground state relaxation. PHYS REV LETT, pp. 1767-1770.
8. M.S. Bigelow, N.N. Lepeshkin and R.W. Boyd (March 21, 2003). Observation of ultraslow light propagation in a ruby crystal at room temperature. PHYS REV LETT, 113903.
9. M.S. Bigelow, N.N. Lepeshkin and R.W. Boyd (July 11, 2003). Superluminal and slow light propagation in a room-temperature solid. SCIENCE, pp. 200-202.
10. E. Baldit et al (Sept. 26, 2005). Ultraslow light propagation in an inhomogeneously broadened rare-earth ion-doped crystal. PHYS REV LETT, 143601.
11. A. Schweinsberg et al (January 2006). Observation of superluminal and slow light propagation in erbium-doped optical fiber. EUROPHYS LETT, pp. 218-224.
12. X. Zhao et al (Oct. 3, 2005). Tunable ultraslow light in vertical-cavity surface-emitting laser amplifier. OPT EXPRESS, pp. 7899-7904.
13. M. González-Herráez, K.-Y. Song and L. Thévenaz (Aug. 22, 2005). Optically controlled slow and fast light in optical fibers using stimulated Brillouin scattering. APPL PHYS LETT, 081113.
14. Y. Okawachi et al (April 18, 2005). Tunable all-optical delays via Brillouin slow light in an optical fiber. PHYS REV LETT, 153902.
15. J.E. Sharping, Y. Okawachi and A.L. Gaeta (Aug. 8, 2005). Wide bandwidth slow light using a Raman fiber amplifier. OPT EXPRESS, pp. 6092-6098.
16. D. Dahan and G. Eisenstein (Aug. 8, 2005). Tunable all optical delay via slow and fast light propagation in a Raman assisted fiber optical parametric amplifier: A route to all optical buffering. OPT EXPRESS, pp. 6234-6249.