Photonic crystal fiber lasers have the potential to revolutionize rare-earth-doped fiber lasers in high-power operation.
J. Limpert, A. Liem, T. Schreiber, F. Röser, H. Zellmer and A. Tünnermann, Friedrich Schiller Universität Jena,
Institute of Applied Physics
The first rare-earth-doped fiber lasers, which produced a few milliwatts at a wavelength of around 1 μm, were operated in the early 1960s. For the next several decades, fiber lasers were little more than a low-power laboratory curiosity. Recently, however, with the advent of reliable, high-brightness, diode-pumped lasers — and of double-clad fibers to facilitate coupling the pump light into the fiber — they are entering the realm of kilowatt powers with diffraction-limited beam quality (Figure 1).
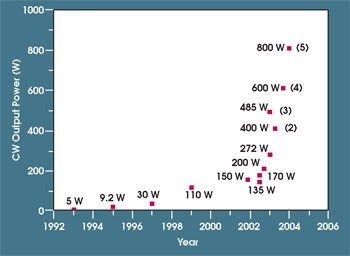
Figure 1. The diffraction-limited power available from fiber lasers has increased dramatically during the past several years, but conventional fiber lasers are reaching their limit because of constraints from nonlinear optics and material damage.
Compared with bulk solid-state lasers, the chief advantage of fiber lasers is their outstanding heat-dissipation capability, which is due to the large ratio of surface to volume of such a long, thin gain medium. As a result, thermal distortion of the beam is negligible, and the beam quality depends solely on the physical design of the fiber. Fiber lasers and amplifiers have a very high single-pass gain; therefore, low laser thresholds can be efficiently pumped with diode lasers. Moreover, the broad gain bandwidth, and the compactness, robustness and simplicity of operation make fiber lasers attractive for a host of applications.
However, nonlinear effects that restrict the ultimate power of fiber lasers, such as stimulated Raman scattering, scale as the product of power density and fiber length.1 Novel fibers with reduced nonlinearity have led to remarkable power increases during the past two years, but further increases will necessarily entail larger-mode-area fibers — to reduce the power density — and/or shorter fibers.2-5
The novel properties of photonic crystal fibers (PCFs) lead to significantly larger mode areas, which enables upward power scaling of both continuous-wave and pulsed laser systems.
Most applications require diffraction-limited beam quality, which translates as a maximum core diameter of ~15 μm in a conventional, step-index fiber. A larger core would normally lead to the propagation of higher-order transverse modes. However, several techniques have been demonstrated to ensure single-mode operation in slightly multimode fibers, such as the application of bending losses, which are significantly higher for higher-order transverse modes than for the LP01 mode.6 Therefore, a properly coiled fiber can prefer single-mode operation in a fiber that would otherwise be slightly multimode. Other approaches depend on a preferential gain to the fundamental mode, created by an optimally overlapping rare-earth dopant distribution.7
Alternatively, one can optimize the design of a multimode fiber to avoid scattering of the fundamental to higher-order modes combined with a careful excitation of the fundamental mode at the beginning of the fiber; e.g., by inserting tapered sections.8,9 By applying these techniques, experimentalists have extracted diffraction-limited output from a step-index, multimode fiber with a mode-field diameter as large as 30 μm.10
However, robust and environmentally stable fundamental mode operation is possible only in a true single-mode fiber. Therefore, single-mode fibers with large mode areas would be a significant achievement. Microstructuring the fiber adds several attractive properties to conventional fibers, which is why PCFs, or “holey fibers,” are currently the subject of intense research.11 These fibers have several interesting and novel features, including the ability to be strictly single-mode over a large wavelength range.12 In other words, the mode area of a PCF theoretically can be scaled to infinity at a given wavelength.
The cladding of one of the PCFs we are developing at Friedrich Schiller Universität Jena in Germany, together with Crystal Fibre A/S of Birkerød, Denmark, consists of a triangular array of airholes that have a diameter d and pitch Λ (Figure 2). Intuitively, one can imagine that the airholes decrease the “average” refractive index of the cladding so that light is guided in the core by modified total internal reflection. Analogous to conventional step-index fibers, a normalized frequency parameter (V-parameter) for a photonic crystal fiber can be defined.13 For a photonic crystal fiber having a core formed from a single missing hole, the V-parameter is shown on the left side of Figure 2.
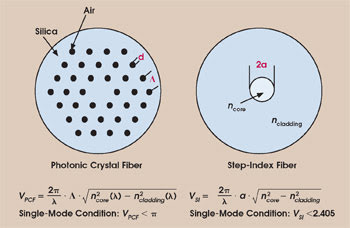
Figure 2. In a photonic crystal fiber (or “holey fiber”), the refractive index of the cladding is reduced to below that of the core by a system of holes along the fiber's length.
The condition for higher-order-mode cutoff can be formulated as VPCF = π.13 In contrast to step-index fibers, the effective index of the cladding region of a PCF is strongly wavelength-dependent (Figure 3). If the ratio of wavelength of the guided mode to hole-to-hole distance, λ/Λ, approaches zero, then the effective cladding index approaches the effective core index.
One can show mathematically that these unusual dispersion properties of the cladding, taken together with the single-mode condition of Figure 2, led to the behavior shown in Figure 4. Here, the curved line across the lower right side of the plot indicates where the single-mode condition is met; above the line, only single-mode propagation is possible.
For any fiber whose d/Λ ratio is less than about 0.45, all wavelengths will propagate in a single mode. Such fibers are termed to be “endlessly single-mode.” It’s important to note that this calculation applies only to PCFs with a hexagonal pattern of airholes, with a single airhole missing. To simplify the calculation, we assume that the cladding is infinitely thick, but this simplification introduces a negligible discrepancy with the results in real fibers.
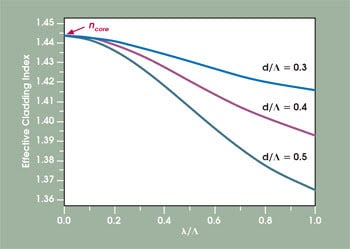
Figure 3. The effective refractive index of a PCF’s cladding has a very strong wavelength dependence.
A more intuitive explanation of these unusual guiding properties is to consider the airholes (diameter d, spacing Λ) as a modal filter or modal sieve.14 Because of the evanescence of light in air, the holes are strong barriers and can be analogous to the wire mesh of the sieve. The fundamental transverse mode with a lobe dimension of ~2Λ fits into the core, and it cannot escape through the too-narrow silica gaps between the airholes.
In contrast, the higher-order modes have significantly smaller lobe dimensions and can therefore slip through the gaps. It becomes clear that, if the relative hole size d/Λ increases, more and more higher-order modes become guided. Thus, the cladding geometry alone determines the number of guided modes, and no higher-order modes are guided at all if d/Λ is less than 0.45. This last observation is truly independent of wavelength — and independent of core diameter. Thus, if a hexagonal PCF whose core is a single missing airhole meets the condition d/Λ <0.45, its core can theoretically become arbitrarily large, and the fiber will still be single-mode.
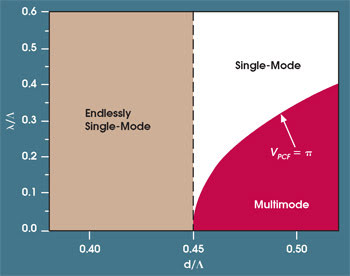
Figure 4. If the holes in the cladding have a diameter-to-spacing ratio of less than 0.45, the fiber is “endlessly single-mode”; i.e., a single-mode fiber at any wavelength.
Of course, the scaling of the core size is limited by increasing propagation losses.15 If the V-parameter of the photonic crystal fiber is smaller than 1, confinement of the mode is too weak and leakage occurs through the fiber’s finite cladding. On the other hand, if the value λ/Λ becomes too small (<0.1), scattering losses resulting from longitudinal nonuniformities increase; e.g., losses due to micro- and macrobending and dielectric imperfections play an important role. An experiment taking all of these design considerations into account has demonstrated the realization of “one-missing-hole” fibers with a mode-field diameter of about 26 μm in the 1.5-μm region with low bending loss.16
The gain medium of a fiber laser can be fabricated by replacing the pure silica core with a rare-earth-doped rod. In general, the core is co-doped with fluorine to compensate for the increase in refractive index caused by the rare-earth ion. This ensures that the refractive index of the rod closely matches that of the silica cladding. The refractive-index step can be reduced to ~10–5 even at relatively high ytterbium doping levels, so that the guiding properties are determined by the photonic crystal structure surrounding the core and not by any index step resulting from the dopants.
If further scaling of the mode area of single-mode fibers is desired, improved large-mode-area PCF designs based on cores formed by more than one missing airhole might be considered. Numerical simulations and experiments have shown that a three-missing-hole design can realize 30 percent larger mode-field diameters than a one-missing-hole fiber — with unchanged propagation losses (Figure 5).17

Figure 5. A PCF can be fabricated by removing an arbritrary number of air holes. Shown are a few examples of one, three or seven missing holes. The fiber's core diameter and, hence, the diffraction-limited power increase as more holes are removed.
Taking this even further, a seven-missing-hole design would allow mode-field diameters of more than 35 μm with low bending losses. Even larger mode-field diameters are possible if bending losses remain small; i.e., if the absorption length is short enough that the device requires no bending of the fiber — typically for fiber lengths of around 1 meter or shorter.18 As stated above, the criterion that a fiber must meet to be endlessly single-mode is d/Λ <0.45 for the fiber with one hole missing. For the fibers with three and seven missing holes, the criteria are d/Λ <0.25 and d/Λ <0.15, respectively.
Another advantage of microstructuring a fiber is the possibility of forming an air-cladding region to create double-clad fibers.19 In a single-clad fiber, pump light must be coupled directly into the low-numerical-aperture core, but in a double-clad laser, it can be more efficiently coupled into the high-numerical-aperture inner cladding. Double-clad PCFs can be achieved by surrounding the inner cladding with a web of silica bridges that are substantially narrower than the wavelength of the guided radiation. The result is a significantly greater index difference between the inner and outer claddings than can be achieved in conventional fibers.20 This reduces the diameter of the inner cladding while still maintaining sufficient numerical aperture for efficient pumping.
The advantage of shrinking the inner cladding is that the overlap ratio of the core to the inner cladding increases, leading to shorter absorption lengths — or higher thresholds for nonlinear effects. Alternatively, the large index step between the inner and outer claddings can produce very large (~0.8) numerical apertures if the diameter of the inner cladding is not reduced, and these apertures greatly reduce the need for sophisticated coupling optics of high-power diode laser stacks into the active fiber. Furthermore, no radiation has direct contact with the coating material, which avoids another common problem with conventional fibers.
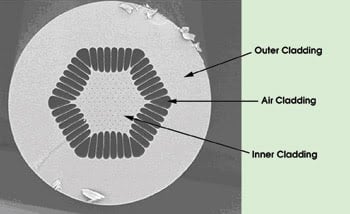
Figure 6. PCFs can be fabricated as double-clad fibers, facilitating coupling pump power into the fiber. In this case, the air space crossed by tiny glass bridges serves as the outer cladding.
In a cross section of the first ytterbium-doped large-mode-area PCF pushed to high power levels, the fiber has a 28-μm single-mode core — three missing holes — and a 150-μm-diameter inner cladding with a NA of >0.55 surrounded by an air-cladding region (Figure 6).21 Up to 80 W of output are extracted from a 2.3-m fiber. This result could be scaled up to 260 W out of a 4-m-long fiber with a similar core design but slightly modified inner cladding dimensions. Figure 7 illustrates the output characteristic of this laser.
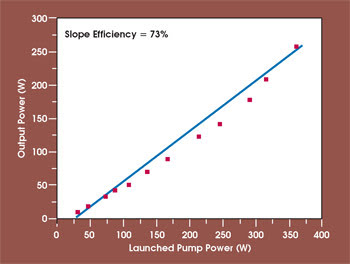
Figure 7. A PCF laser similar to the one in Figure 6 produced 260 W of diffraction-limited output.
These results give us confidence in our extrapolation of the diffraction-limited output power that could be obtained from an air-cooled PCF laser, taking into account limitations due to damage, thermal loading and nonlinear optics. This calculation assumes a microstructured single-mode core with a mode-field diameter of 35 μm (Figure 8). The surface damage of fused silica is approximately 2 GW/cm2, although this value is significantly lower in doped glasses. Damage thresholds greater than 500 MW/cm2 for doped glass have been demonstrated experimentally, and this value leads to a damage threshold of about 4.6 kW in a core with a mode-field diameter of 35 μm (the black line in Figure 8).
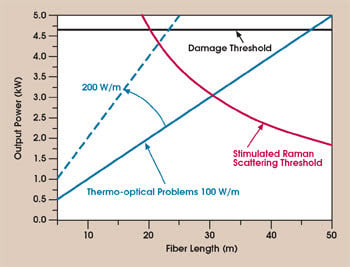
Figure 8. This graphic shows the potential diffraction-limited power available from a PCF laser with a 35-μm core. With passive cooling, an output power up to 3 kW should be possible; if forced-air or water cooling are used, it could be as high as 4 kW.
Detailed investigations of the thermo-optical behavior of air-clad rare-earth-doped microstructured fibers have shown that these fibers have basically the same heat dissipation capabilities as conventional double-clad fibers if the air-cladding region is properly designed.22 An extracted power of 100 W/m is experimentally demonstrated without thermal problems out of air-cooled fibers with an outer diameter larger than 400 μm.
This value is assumed as the limit in Figure 8 (solid blue line). The calculated threshold of nonlinearity (stimulated Raman scattering) as a function of the fiber length is based on several experimental results that are supported by numerical simulations (red line). This analysis leads to the conclusion that it is possible to extract a power of ~3 kW from an air-cooled, single-mode PCF laser. If more sophisticated cooling techniques are applied — e.g., forced-air cooling or passive water cooling — the extracted power can be easily enhanced to 200 W/m without thermo-optical issues (blue dashes).
As can also be seen in Figure 8, this could produce a possible output power of 4 kW. Because of the recent developments of reliable high-brightness all-solid-state pump sources and to recent advances in fiber manufacturing technology, we fully expect that these power levels will soon be demonstrated in the laboratory.
In conclusion, rare-earth-doped PCFs offer several unique properties that allow them to be scaled to higher power than conventional fiber lasers. The most remarkable of these properties are significantly larger single-mode core sizes, which can lead to a reduction of nonlinearity by an order of magnitude compared with conventional step-index single-mode fibers, as well as an air-cladding region that allows significantly larger numerical apertures of the inner cladding.
Indeed, we believe that PCF lasers have the potential to revolutionize rare-earth-doped fiber lasers in high-power operation.
Acknowledgment
We thank the German Ministry of Education and Science for its financial support and Crystal Fibre A/S for its fruitful collaboration.
References
1. G.P. Agrawal (1995). Nonlinear Fiber Optics, Academic Press.
2. N. Platonov et al (1993). 400W low-noise singlemode CW Ytterbium fiber laser with an integrated fiber delivery. Conf. on Lasers and Electro-Optics. OSA, postdeadline paper CThPDB9.
3. www.spioptics.com.
4. J. Limpert et al (2003). 500 W continuous-wave fibre laser with excellent beam quality. ELECTR. LETT., 39:8, p. 645.
5. C. Liu et al (2004). 810-W single transverse mode Yb-doped fiber laser. ASSP, postdeadline paper PD2.
6. J.M. Sousa and O.G. Okhotnikov (1999). Multimode Er-doped fiber for single-transverse-mode amplification. APPL. PHYS. LETT. 74, p. 1528.
7. J.P. Koplow et al (2000). Singlemode operation of a coiled multimode fiber amplifier. OPT. LETT., Vol. 25, p. 442.
8. M.E. Fermann (1998). Singlemode excitation of multimode fibers with ultrashort pulses. OPT. LETT., Vol. 23, p. 52.
9. J.A. Alvarez-Chavez et al (1999). Mode selection in high power cladding pumped fiber lasers with tapered sections. Conf. on Lasers and Electro-Optics, p. 247.
10. A. Galvanauskas (2001). Mode-scalable fiber-based chirped pulse amplification systems. IEEE JOURN. ON SELECTED TOPICS IN QUANTUM ELECTRONICS, Vol. 7, p. 504.
11. A. Bjarklev et al (2003). Photonic Crystal Fibres. Kluwer Academic Publishers.
12. T.A. Birks et al (1997). Endlessly singlemode photonic crystal fibre. OPT. LETT., Vol. 22, pp. 961-963.
13. N.A. Mortensen et al (2003). Modal cut-off and the V-parameter in photonic crystal fibers. OPT. LETT., Vol. 28, p. 1879.
14. P. Russell (2003). Photonic crystal fibers. SCIENCE, Vol. 299, p. 358.
15. N.A. Mortensen and J.R. Folkenberg (2003). Low-loss criterion and effective area considerations for photonic crystal fibers. J. OPT. A: Pure Appl, 5, p. 163.
16. M.D. Nielsen et al (2003). Singlemode photonic crystal fibre with effective area of 600 μm2 and low bending loss. ELECTR. LETT., 39:25, p. 1802.
17. N.A. Mortensen et al (2003). Improved large-mode-area endlessly singlemode photonic crystal fibers. OPT. LETT., Vol. 28, p. 393.
18. J. Limpert et al (2004). Extended large-mode-area singlemode microstructured fiber laser. Conf. on Lasers and Electro-Optics, San Francisco, session CMS.
19. E. Snitzer et al (1998). Double Clad, Offset Core Nd Fiber Laser. Conf. on Optical Fiber Sensors, PD5.
20. W.J. Wadsworth et al (2003). High power air-clad photonic crystal fibre laser. OPT. EXPRESS, Vol. 11, pp. 48-53.
21. J. Limpert et al (2003). High-power air-clad large-mode-area photonic crystal fiber laser. OPT. EXPRESS, Vol. 11, pp. 818-823.
22. J. Limpert et al (2003). Thermo-optical properties of air-clad photonic crystal fiber lasers in high power operation. OPT. EXPRESS, Vol. 11, pp. 2982-2990.
Meet the authors
The authors work in the fiber and waveguide laser group at the Institute of Applied Physics, Friedrich Schiller Universität Jena in Germany, Drs. Jens Limpert and Andreas Liem as postdoctoral students; Thomas Schrieber and Fabian Röser, PhD students; and Dr.?Holger Zellmer, group leader. Prof.?Dr. Andreas Tünnermann is leader of the institute and of the?Fraunhofer Institute for Applied Optics and Precision Mechanics.