Developed over a century ago to measure the angular distribution of light, conoscopes are becoming an increasingly valuable inspection tool for emerging technologies.
STEVE ECKHARDT AND KARLY LUNDA, ECKHARDT OPTICS
After languishing for the first century of their existence, conoscopes have become essential to the production of consumer products in an increasing number of industries. What began in 1911 as simple scientific curiosities designed for liquid crystal evaluation grew in prominence when liquid crystals became the dominant display technology in the 1980s. In the last five years, conoscopes have evolved to influence burgeoning technologies such as facial recognition, virtual and augmented reality (VR/AR), high-speed scatterometers, and display testing. The expanding use of these tools calls for another look at their basic design, specification, and application.

A rendering of a cross section of a 60° half-angle conoscope. Courtesy of Eckhardt Optics.
A conoscope lens is constructed of a group of individual glass elements that may also be called lenses. This can be confusing. So, within the context of this article, “lens” will refer to the conoscope, while “lens elements” will refer to the lenses that make up the conoscope.
In simple terms, a conoscope is used to observe the angular distribution of light. It may also be thought of as a wide-angle lens with the entrance pupil in front. In
its most common form, it is an f-theta
(aka Fourier transform) lens followed by
a relay lens, as illustrated in Figure 1.
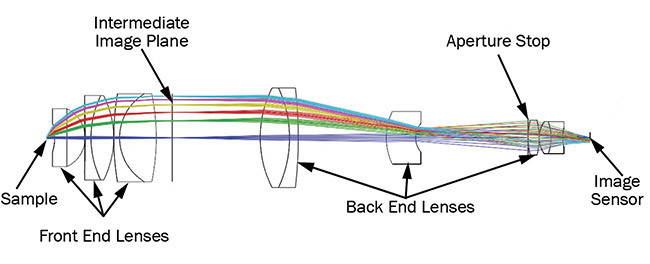
Figure 1. A schematic of a conoscope lens. Courtesy of Eckhardt Optics.
The first group of lens elements in a conoscope includes an external pupil, and it maps the angle of incoming light onto a linear distance on the internal image plane. In other words, as the angle between a light ray and the optical axis of the lens increases, so does the distance from the optical axis to the point where the ray intersects the image plane. Doubling the incoming angle also doubles
the distance from the axis to the intersection, which is known as the image height.
Often, the image height for the maximum ray angle is too large to accommodate an affordable image sensor, which
requires the size of the image to be reduced. This is the main function of a conoscope’s second lens group. The second group removes residual image errors left by the first group and may also include the aperture stop for the lens if there is no physical aperture in front of the first group.
While these factors define the basic bones of a conoscope, the dimensions of these devices vary widely, ranging from 350 mm long to small lenses that measure only 120 mm in size. A conoscope
designed to evaluate a VR/AR system,
for example, would look very different from one designed to measure the level
of polish on the leading edge of an airplane wing.
Mapping liquid crystals
The evaluation of liquid crystals is the oldest application of conoscopes and remains the most familiar. LCDs are characterized by variable brightness depending on angle of view, and they exhibit variations in contrast and color shift.
All of these qualities can be mapped by attaching a conoscope to a camera to
produce an image displaying a circle
that represents a near-hemisphere of
performance, with each pixel representing a specific combination of polar angle
and azimuth.
If the LCD is put into its bright state, the imaged circle should appear almost uniformly white, while a uniformly black circle should result from putting the LCD into its dark state. The ratio of these images is a map of the LCD contrast. Color shift can be mapped similarly.
When applying this inspection method, it is important that the lens not physically contact the LCD. This makes it imperative to have an aperture stop within the lens that is projected out in front as the entrance pupil. In practice, this allows placement of the conoscope so that the entrance pupil is located in the plane of the liquid crystal material.
Emerging applications
Inspection of facial recognition subsystems is a more recent application for conoscopes. To accurately map facial contours, these systems often incorporate a diffractive optical element (DOE) to direct each beam of a two-dimensional vertical-cavity surface-emitting laser (VCSEL) array into a dot pattern on a human face. To function properly, each laser must emit the same amount of light and the DOE must accurately direct that light in the required direction.
Conoscopes can help ensure this by mapping emitted beams onto corresponding pixels in an image sensor to compare the position and brightness of each beam against a standard. The conoscope requires no aperture; the facial recognition subsystem under test serves this purpose. Because the laser beams are focused near the user’s face, however, the conoscope must be designed for a virtual object. That is, the light appears to the lens to have come from somewhere inside the lens.
Conoscopes offer further benefits to the design of scatterometers, which are used to measure the angular distribution of light scattered by a surface. When paired with a conoscope, scatterometers can record nearly an entire hemisphere in a single frame. Compared to scanning scatterometers that may take tens of seconds per scan, conoscopic instruments permit capture of 100 fps, potentially improving measurement speed by several orders of magnitude.
One important consideration when
applying conoscopic scatterometers is
that they require a fairly large number of lens elements. So light scattering by antireflection coatings can become a problem. The problem may be compounded if the application involves using a light source for measuring scatter of reflected light because the light must pass through the first group of lens elements, from the internal image plane to the sample. If the antireflection coating reflects even 0.25% of the light, then reflections from the elements of the front group can appear in the image. A dark-field calibration can help subtract these reflections out, but the subtraction is never perfect. Consequently, scanning scatterometers may be preferable for measurements in which a large dynamic range is required.
Inspection of VR/AR components is another rapidly growing market for conoscopes. Each headset includes two subsystems consisting of a display and an eyepiece that present an image to the user’s eye. Evaluation of these systems requires an instrument that mimics the human eye. Specifically, it must have a pupil in the correct location and be capable of resolving pixels over the entire display, which may cover a wide field of view. To make analysis easier, it should also map incoming ray angles linearly to image height.
Another significant nuance with VR/AR inspection is that the devices must accommodate both near-sighted and far-sighted users. So the inspection system must be able to zoom to adjust for various object distances. Most systems for this application cover object distances from 250 mm in front of the lens to infinity. But some are capable of focusing from −100 mm (i.e., inside the lens) to infinity to +100 mm (i.e., in front of the lens). Optometrists speak in terms of diopters, which have units of inverse meters. Zero diopters (0 D) corresponds to a plane parallel plate or an infinite object distance, and 10 diopters (10 D) corresponds to
0.1 m or 100 mm. In these units, a normal system adjusts from 0 to 4 D, whereas a really wide-range system ranges from −10 to +10 D.
Design considerations
When specifying a conoscope, the most important attribute to remember is the Lagrange invariant, or conservation of etendue. In plain terms, violating these rules would be similar to fitting 10 lbs of material into a 1-lb bag. Basically, you cannot have a wide-angle conoscope with a large pupil connected to a small image sensor.
As applied to conoscopes, the equation is: Φp * sinΘ = Φi * NAi.
As shown in Figure 2, Φp represents the diameter of the entrance pupil, Θ is the half field of view of the conoscope, Φi
is the diameter of the image, and NAi
(sin Θi) is the numerical aperture of the lens. The NA of a lens is approximately half the inverse of the f/# (= 0.5/f/#).
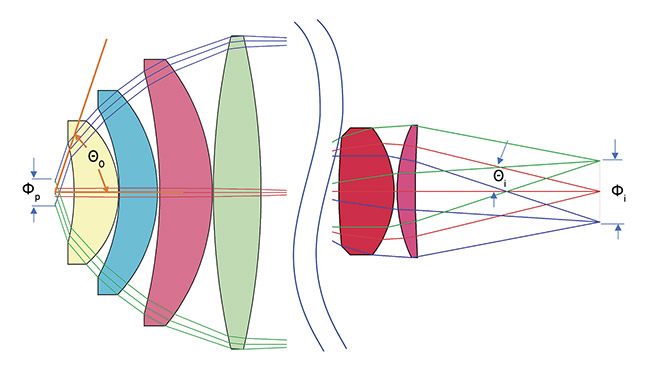
Figure 2. A conoscope view showing the variables used in the Lagrange equations. Courtesy of Eckhardt Optics.
Understanding this is critical when specifying a conoscope. Once the aperture
(or sample size) and field of view are chosen, then either the image size or the f/#
of the lens can be chosen, but not both. Take, for example, a conoscope with
an 80° half field of view and a 4-mm-diameter aperture. Designing the lens
for a 1/3.2-in. (3 × 4 mm) image sensor will require a lens with an NAi of 1.3. Because lens designs start to become challenging at NA 0.25 (f/2), meeting this hypothetical requirement would be an impossibility.
The working distance (WD) from the sample or aperture to the front of the conoscope lens is another specification that can raise potential issues. Engineers who design inspection systems like to have a lot of room between the device under test and the lens. This makes sense. Unfortunately, when they request a WD of 50 mm and a half field of view of 75°, a quick calculation shows that the first surface of the lens must be about 380 mm in diameter, as demonstrated by the following equation: Φ1 = Φp + 2 * tanΘ =
6 + 2 * tan(75°).
Even worse, as Figure 3 illustrates, the first surface cannot bend the rays very far, which requires the conoscope to be about twice the diameter of the first surface. Faced with the prospect of a multimillion-dollar lens, most engineers would instead favor a more reasonable WD.
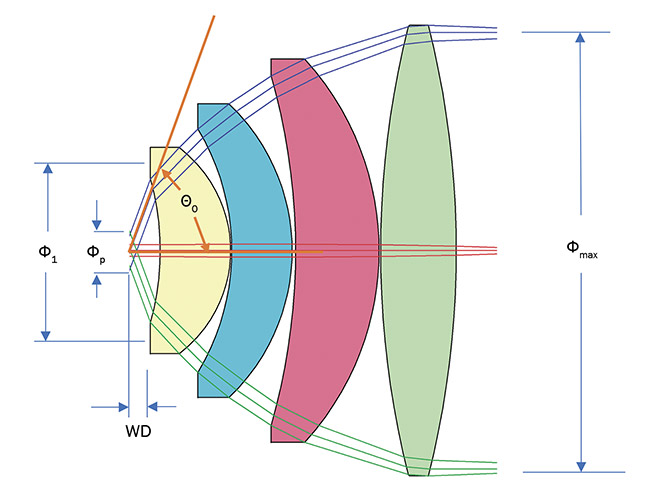
Figure 3. A conoscope view showing the variables used in the sizing equations. Courtesy of Eckhardt Optics.
While these first two rules of design are based on basic physics and geometry, a third rule is more of a heuristic and provides a rough idea of the challenges of designing a conoscope. The third rule is defined by the following equation: x = Φp * Θ/OD, where OD is the outside diameter of the conoscope and x represents the degree of difficulty. If Θ is given in degrees in this equation, then a value of less than 2 for x represents an easy design, while values exceeding 5 or more correspond to a difficult one. There are other factors that can make design more difficult. A large (>70°) field of view, a wide wavelength range, a large NA (fast f/#), or a large zoom range would add to the difficulty.
Futurescope
As more applications for conoscopes appear, it is vital to understand the principles necessary for designing a functional instrument. The specifications above represent a theoretical limitation for a conoscope lens. While specifications are often incomplete, a basic understanding of conoscope design principles can still enable development of a highly effective instrument.
This 100-year-old technology, which commonly comprises an f-theta (Fourier transform) lens followed by a relay lens, is offering innovative new approaches for product testing. The last decade alone has seen the formerly humble conoscope rise to a newfound prominence in the realm of consumer product inspection.
Meet the authors
Steve Eckhardt, Ph.D., is an optical engineer at Eckhardt Optics and, when not reading or spending time with his grandkids, he serves as president of the company and its chief lens designer. In addition to a doctorate in optics from the University of Arizona, he has 40 years of photonics industry experience.
Karly Lunda is Eckhardt Optic’s communications and graphic design specialist. When she is not translating complex photonics topics for a broader audience, you can find her hiking by Lake Superior.