This approach holds promise for advancing laser remote sensing, fluid dynamics and profilometry.
CARMELO ROSALES-GUZMÁN, UNIVERSITY OF THE WITWATERSRAND; ANICETO BELMONTE, POLYTECHNIC UNIVERSITY OF CATALONIA; AND JUAN P. TORRES, ICFO-THE INSTITUTE OF PHOTONIC SCIENCES AND THE POLYTECHNIC UNIVERSITY OF CATALONIA
As a result of technological advances in recent years, researchers have at their disposal devices capable of tailoring — with almost unlimited freedom — the shape of beams of light. Computer-controlled spatial light modulators (SLMs) and digital micromirror devices (DMDs) are some of the most popular devices with such capabilities. They are invaluable tools in the generation of optical beams with a transverse varying phase structure, otherwise known as structured, sculpted or engineered fields. Two examples of these structured fields are Laguerre-Gauss and Hermite-Gauss beams.
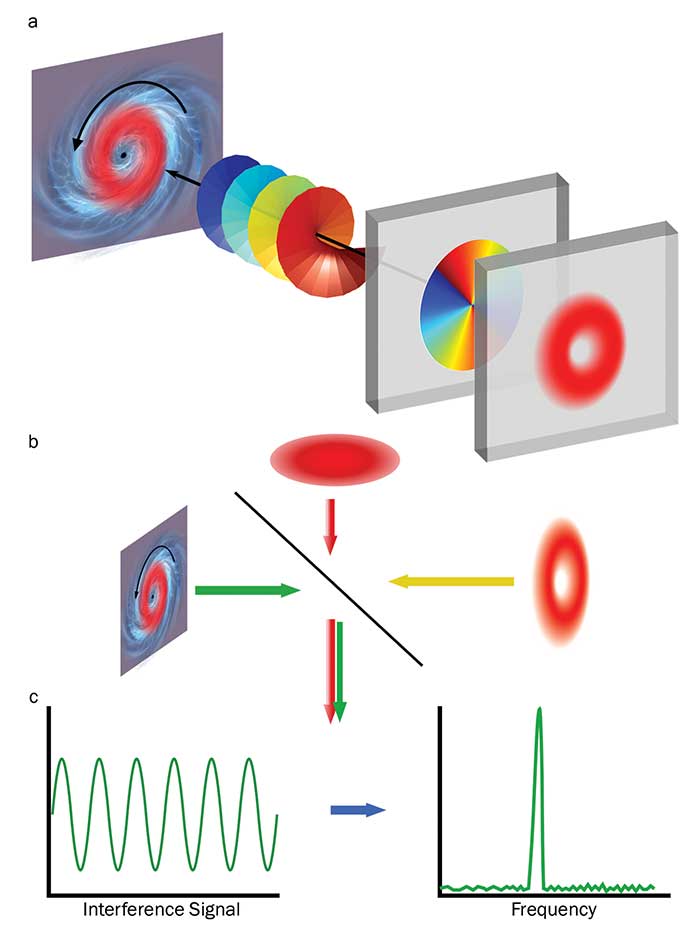
Figure 1. The angular velocity of targets describing a circular motion can be measured directly with a vortex beam (a). The backscattered signal is interfered with a reference signal (a Gaussian beam, for example) to extract the desired information (b). The interference signal is Fourier transformed to obtain a frequency peak that is directly related to the target’s velocity (c). Courtesy of Carmelo Rosales Guzman.
Structured beams are routinely used in many different fields of science and technology1,2. In optical microscopy, optical vortices are a convenient way to shape the light beams as required by some superresolution techniques capable of reaching resolutions far beyond the diffraction limit3. In the field of optical tweezers, the great diversity of existing structured fields have made it possible not only to trap, but also to guide micron-sized particles along various 2D and 3D trajectories4. The use of optical beams with different spatial shapes as information carriers provides a way to explore new avenues for increasing the bit rate of optical communications systems5,6. The potential advantages of using beams with a tailored complex wavefront for measuring velocities and fluid vorticity have broad applications in laser remote sensing — to measure velocities and fluid vorticity — and in the high-resolution profilometry — to measure surface profiles.
The Doppler effect, the frequency shift that acquires a light beam when scattered back from a moving object, is a well-known technique used to monitor the position and speed of moving targets. The Doppler effect observed when the illumination source is a Gaussian beam with nearly a flat wavefront provides information on the velocity of the target along the direction parallel to the beam’s propagation axis — that is, the direction of the energy flow (Poynting vector) of the optical beam.
Some approaches to overcome this drawback have been developed, such as considering multiple Gaussian beams propagating along different directions to measure the corresponding velocity components. In general, these schemes require the use of several light sources, or fast mechanical realignment of the direction of propagation of the laser beam, which makes its implementation cumbersome. On the contrary, when using structured light as the illumination source, the light reflected from the target can also carry information about the velocity of the target in the transverse plane. This is due to the fact that tailoring phase gradients in the optical beam corresponds to the additional introduction of flows of energy perpendicular to the direction of propagation of the optical beam7.
That information is reflected in the appearance of what can be called a transverse Doppler frequency shift associated with the presence of a transverse component of the Poynting vector8, or in other cases, the change of position of the target in the plane perpendicular to the propagation axis of the illuminating beam.
Measuring the interference signal
The relationship between this transverse Doppler shift and the transverse component of the velocity allows the unique determination of the full value of the velocity. In principle, the illumination beam can take any structured phase profile; however, information about the type of movement can help to tailor the most appropriate phase profile7,9.
For instance, for targets rotating at constant angular velocity, azimuthally varying phases such as those present in Laguerre-Gaussian vortex beams adapt perfectly to their motion (Figure 1a). To extract the desired information, the backscattered light is made to interfere with a reference beam (Figure 1b). The intensity of the interference signal is measured and Fourier transformed to obtain a frequency peak (Figure 1c) from which the transverse component of the velocity can be easily obtained.
One can envision complex systems based on structured light beams capable of measuring simultaneously all components of velocity, longitudinal (νll) and transverse (ν⊥). The basic idea has been demonstrated recently in a proof of concept experiment10. Here, particles in a 3D helical motion were illuminated sequentially with a Gaussian and a vortex beam (Figure 2a) to determine the full velocity vector. In this scheme, the Gaussian beam is used to measure the longitudinal component and the vortex beam is used to measure the transverse component of the velocity, in this case the angular velocity. Moreover, spatial light modulators can also be used to actively change from one hologram to another, a feature that can be exploited to determine the direction of motion. Currently this measurement is done through the use of acousto-optic modulators, electro-optic frequency shifters or rotating waveplates, which are commonly restricted to particular beam sizes and specific frequencies. Here, the concept is to actively change the holograms displayed on the spatial light modulator to upshift or downshift the Doppler frequency generated by the moving target11. The direction of motion would be determined after comparison of both frequencies, since a downshift will be observed if the target moves in the same direction of the dynamic phase (Figure 2b).
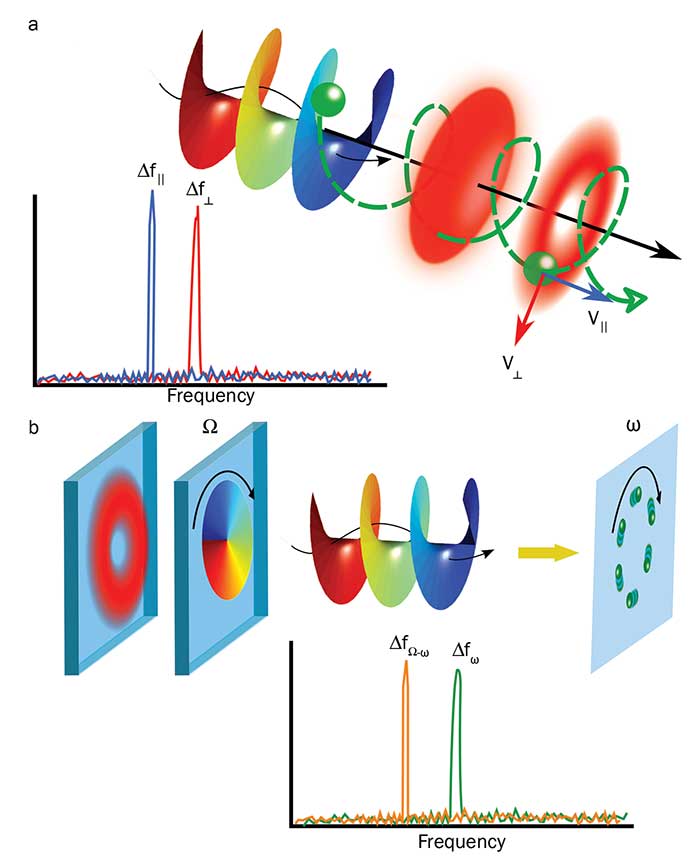
Figure 2. A particle moving in a 3D helical motion can be interrogated simultaneously with a vortex and a Gaussian beam (a). As a consequence, a longitudinal and a transverse Doppler shift will appear. A rotating phase profile illuminating a rotating particle will upshift or downshift the Doppler frequency corresponding to the particle’s motion, which can be used to determine its direction of motion (b). Courtesy of Carmelo Rosales Guzman.
Measurement of fluid vorticity
The method described above could impact other areas of research such as in fluid dynamics, where it offers the possibility to measure in a direct way the vorticity in fluids12. Vorticity is a vector field that contains information about the tendency of a fluid to rotate. Well-established techniques for estimating the vorticity are based on computing the curl of the velocity vector. In this approach, uncertainty errors on the velocity affects directly the accuracy of the vorticity. Furthermore, determining the full velocity vector represents a cumbersome task. In contrast, when a certain region of the fluid is illuminated with a vortex beam, the backscattered light generates a spectrum of frequency shifts that contains information about the velocity at every point along the ring of light (Figure 3a). Again, to obtain the desired information, the backscattered light is made to interfere with a reference beam and the interference signal is measured with a photodetector. The measured signal in this case is a mixture of different frequencies (Figure 3b). Hence, its Fourier transform forms a histogram of Doppler frequency components (Figure 3c), whose centroid is directly related to the vorticity of the fluid.
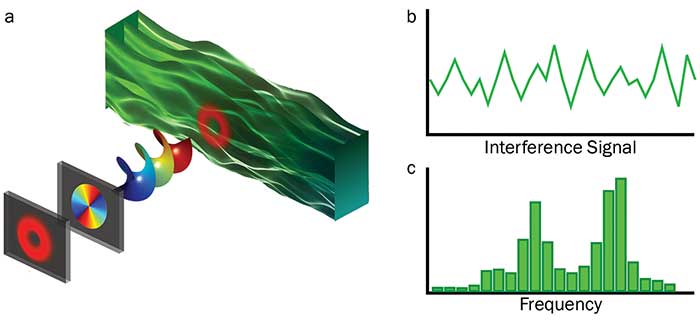
Figure 3. Schematic representation of a vortex beam illuminating a fluid to obtain information of its vorticity (a), the interference signal of the backscattered light and a reference beam (b), and the frequency spectrum from which the vorticity can be measured (c). Courtesy of Carmelo Rosales Guzman.
Accurate measurement of a submicron surface’s profile
The thickness of very thin layers is commonly measured using a common path interferometer13,14. In this configuration, the sample is placed over an engineered ridge with specific width and height. The width is such that half of the illuminating beam straddles the ridge and the other half its base. As a result, two beams traveling along the same path produce a stable interference pattern in the far field, which is due to the difference in height of the surface. The on-axis intensity varies sinusoidally with the height of the ridge, reaching maximum sensitivity for heights equal to 1/8 of the illuminating wavelength (λ). This forces the height of the ridge to be an integer multiple of λ/8, known as the quadrature condition. The sample thickness is determined from the intensity changes it introduces when placed over the ridge (Figure 4a). Unfortunately, the need to fulfill the quadrature condition by constructing a physical ridge limits the use of this technique to certain wavelengths. A method in which the quadrature condition is not imposed by a ridge but rather is passed on to the signal reflected from the sample was recently proposed15. The main idea consists in projecting the reflected light onto appropriately tailored structured light in which the quadrature condition is encoded (Figure 4b). Such projection can be efficiently made with SLMs.
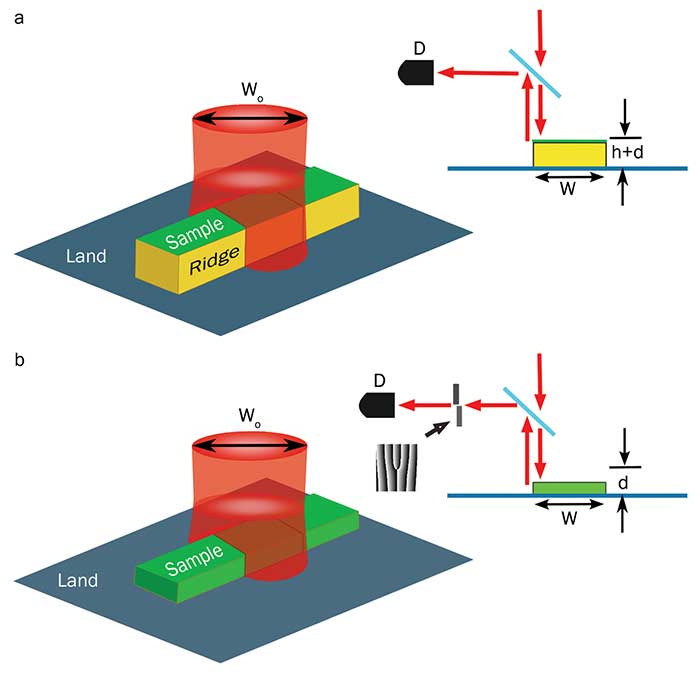
Figure 4. Implementation of the quadrature condition through the construction of a physical ridge (a) by means of projecting the light reflected directly from the sample onto a specifically tailored beam (b). Courtesy of Carmelo Rosales Guzman.
DMDs and diffractive optics hold promise
Structured light beams are invaluable tools that allow the development of new solutions and applications in a great variety of fields such as laser remote sensing, optical communications and superresolution microscopy, to mention just a few.
Here the authors presented novel techniques that could potentially impact the fields of laser remote sensing, fluid dynamics and profilometry. Most of the success of using structured light beams comes from the development of spatial light modulators that have paved the way toward the generation of almost arbitrary structured light beams. However, at present day, the core technology of a spatial light modulator, the liquid crystal, severely limits the use of novel ideas in solutions outside of the lab. For example, their refresh rate is very low (~60 Hz), they are sensitive to polarization, their damage threshold power is low and the wavelength at which they operate can be an issue.
An alternative to the spatial light modulator is the digital micromirror device technology. A DMD consists of an ensemble of several hundred thousand microscopic mirrors, arranged in a rectangular fashion, and integrated in a chip. Each mirror of this ensemble can be rotated digitally to an on or off state, -12° or +12°, respectively. DMDs are cheaper, polarization insensitive and can reach a refresh rate grater that 4 KHz. DMDs are becoming popular and have already demonstrated their potentiality in generating structured light beams. Another option is the use of diffractive optical elements, which can be cheaper and mass produced. The biggest challenge is how to bring these ideas from the lab to real applications and how to combine with current systems to broaden their range of applications.
Meet the authors
Carmelo Rosales-Guzmán, Ph.D., is a postdoctoral researcher in the structured light lab at the University of the Witwatersrand. His research involves the use of structured light for different applications; email: [email protected].
Aniceto Belmonte is a researcher in electromagnetic optics and photonics, working on new methods and techniques for free-space optical communications, laser remote sensing and coherent imaging; email: [email protected].
Juan P. Torres is at ICFO-The Institute of Photonic Sciences and the Polytechnic University of Catalonia. His research focuses on the areas of quantum and nonlinear optics, and fundamentals and applications of structured light; email: [email protected].
References
1. H. Rubinsztein-Dunlop et al. (2017). Roadmap on structured light. J Opt, Vol. 19, Issue 1, 013001.
2. Torres, J. P. and Torner, L. (2011). Twisted Photons: Applications of Light with Orbital Angular Momentum. Wiley-VCH.
3. S.W. Hell (2007). Far-field optical nanoscopy. Science, Vol. 316, pp. 1153–1158.
4. M. Padgett and R. Bowman (2011). Tweezers with a twist. Nature Photon, Vol. 5, p. 343.
5. J. Wang et al. (2012). Terabit free-space data transmission employing orbital angular momentum multiplexing. Nature Photon, Vol. 6, p. 488.
6. A. Trichili et al. (2016). Optical communication beyond orbital angular momentum. Sci Rep, Vol. 6, Article 27674, pp. 2–7.
7. C. Rosales-Guzmán et al. (2013). Experimental detection of transverse particle movement with structured light. Sci Rep, Vol. 3, Article 2815.
8. M.P.J. Lavery et al. (2013). Detection of spinning object using light’s orbital angular momentum. Science, Vol. 341, pp. 537–540.
9. A. Belmonte and J.P. Torres (November 2011). Optical Doppler shift with structured light. Optics Lett, Vol. 36, p. 4437.
10. C. Rosales-Guzmán et al. (2014). Measuring the translational and rotational velocities of particles in helical motion using structured light. Opt Express, Vol. 22, pp. 16504–16509.
11. C. Rosales-Guzmán et al. (2014). Direction-sensitive transverse velocity measurement by phase-modulated structured light beams. Opt Lett, Vol. 18, pp. 5415–5418.
12. A. Belmonte et al. (2015). Measurement of flow vorticity with helical beams of light. Optica, Vol. 2, pp. 1002–1005.
13. D.D. Nolte and F.E. Regnier (Oct 2004). Spinning-disk interferometry: The biocd. Opt Photon News, Vol. 15, pp. 48–53.
14. D.D. Nolte (2009). Invited review article: Review of centrifugal microfluidic and bio-optical disks. Rev Sci Instrum, Vol. 80, 101101.
15. N. Hermosa et al. (2014). Nanostep height measurement via spatial mode projection. Opt Lett, Vol. 39, pp. 299–302.