Full company details

Objective Specifications Drive Performance in Biomedical and Life Sciences Research

BioPhotonics
Jul/Aug 2024Microscope users who better understand the trade-offs in aperture, wave band, and field of view made by objective designers can more effectively balance objective specifications with the rest of their system requirements.


Microscope objectives are critical for a vast range of biological imaging applications, such as isolating cellular dynamics and cancer diagnostics, but designing and building a microscope objective can be a complex and expensive endeavor (opening image). The specifications chosen before starting the design, including numerical aperture (NA) and working distance, can have dramatic effects on the cost and complexity of the design and construction of the microscope system. Because biomedical imaging techniques, such as differential interference contrast microscopy, typically require diffraction-limited performance, specifications that drive optical aberrations, such as astigmatism or curvature of field, are the primary factors in driving the complexity of the design. Understanding these key specifications and the fundamentals of objective design will help a purchaser select the right objective for a particular application and understand how to optimally balance objective specifications with the rest of a system’s requirements.

---

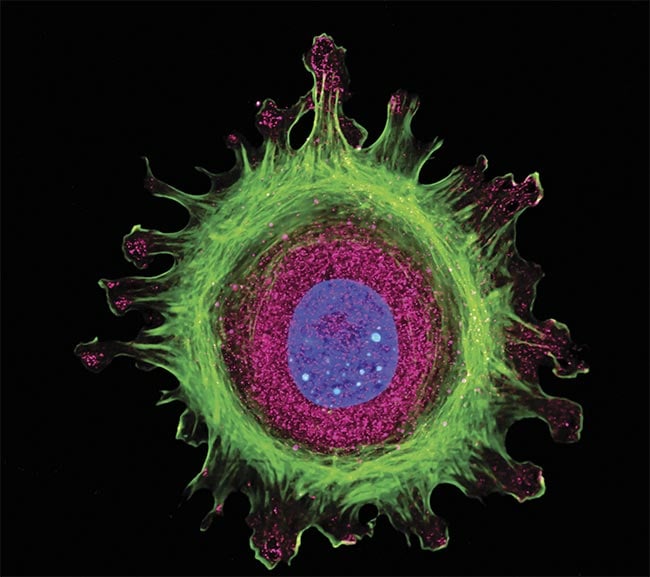
Immunofluorescence of a single human cell, grown in tissue culture, stained with multiple antibodies, and visualized via confocal microscopy. Courtesy of Edmund Optics.

---

Defining parameters

The parameters of a microscope objective must be defined for the purpose of this discussion. The magnification ranges are typically 4× to 120×. Magnifications <4× will not be considered in this article and are in the macro imaging realm, and magnifications >120× are outside the bounds of visible imaging systems. Microscope objectives can be used with a camera sensor or an eyepiece that pairs with a human eye. They can be part of a complex microscope system with multiple objectives on a turret or a specific dedicated imaging system with a single objective.

This discussion will be limited to infinite conjugate objectives that use a tube lens to form a real image with high contrast. These infinite conjugate objectives have become the standard in microscopy for many years because of the advantages offered by the region of collimated (parallel) light between the objective and tube lens for the majority of applications of microscope objectives.

Considering the high magnifications in the microscope objectives, the diffraction limit is an important factor to consider when selecting an objective. The diffraction limit for higher magnifications, such as 4× and larger, is typically larger than the pixels on a sensor or the resolution of the eye through an eyepiece. If the objective does not perform at or near the diffraction limit, the application loses the benefit of better resolution that the higher magnification of the objective provides. Therefore, as the magnification of objectives increases, the NA also must increase to drive the diffraction-limited resolution down and to see finer details in the object. Therefore, diffraction-limited performance is a requirement for the objectives.

Aberrations and complexity

Aberrations are the errors in a design that prevent the rays from perfectly focusing. So, to be diffraction limited, the designer must drive down the aberrations. Correcting these aberrations adds complexity to the design, such as more elements, higher-index glasses, complex shapes, and aspheric surfaces. These complexities result in increased component costs. Balancing aberrations throughout a system also increases the sensitivity of a design to tolerances, or the ultimate configuration of the microscope to be manufactured outside of the design specifications. Errors such as tolerances on element positions in space, index and Abbe tolerances of the materials, and surface figure errors (deviations of the surface from its perfect form) on the elements all become more sensitive as the complexity of the design increases. A typical microscope objective design requires extremely precise optomechanics to position the elements to single-digit micron accuracies to achieve the desired imaging performance.

Three primary factors affect the aberrations in an optical design: aperture, field of view, and wave band. These three specifications will drive the complexity and cost of a microscope objective as well as the difficulty in manufacturing (Figure 1). Aperture is often the most important of these for many biomedical applications since it drives diffraction-limited resolution, but wave band is also important for many biomedical systems, especially for fluorescence microscopy.

---

Figure 1. Trade-offs between the key specifications of microscope objectives drive their complexity and manufacturability, and therefore cost. Courtesy of Edmund Optics.

---

Aperture

Aperture is a critical specification for a microscope objective because it drives the diffraction-limited resolution. The resolving power of the objective (D) is the resolution of a single object space pixel or feature size on an object that the objective can resolve. The Abbe diffraction-limited performance equation is where λ is

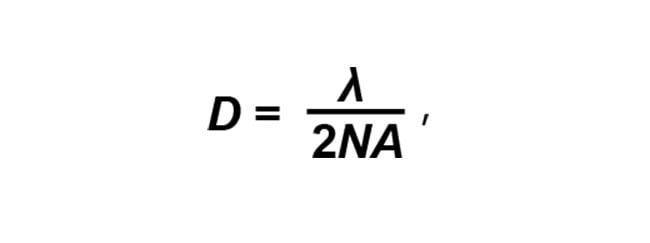
the wavelength of light and NA is the numerical aperture of the objective. For a given wavelength, the larger the NA, the smaller the resolvable features are on the object, such as a tissue specimen.

So, to see fine details in the object, a high NA is needed for the objective. Aperture is typically the most important specification for an objective because it controls the resolving power. Larger NAs also collect more light, which is often the reason for specifying a large aperture in an imaging lens, but for most microscopy applications, the higher resolution is the reason the higher NA is required — more so than the light collection. Using large apertures results in aberrations in the optics that the designer must optimize out of the design. The aperture drives the magnitude of spherical and coma aberrations that are in the design.

However, there is one downside to having a large NA in addition to the complexity it adds to the design and manufacturing: The depth of field of the lens will decrease as the NA increases due to the increased cone angle. Consequently, large NA objectives have very small depths of focus, which makes bringing the object into focus more difficult, narrows what can be seen at one time, and makes aberrations, such as chromatic aberration and field curvature, less tolerable in a design.

To demonstrate how influential aperture is on design complexity, Figure 2 depicts two objectives with an NA of 0.14 on the top and 0.42 on the bottom. The first requires six internal lenses while the second, with 3× the aperture, requires 13 lenses. The top one is also significantly easier to assemble with simple optomechanical constraints, while the second requires difficult active alignment, or a feedback loop and mechanical positioning during assembly of the lenses.

---

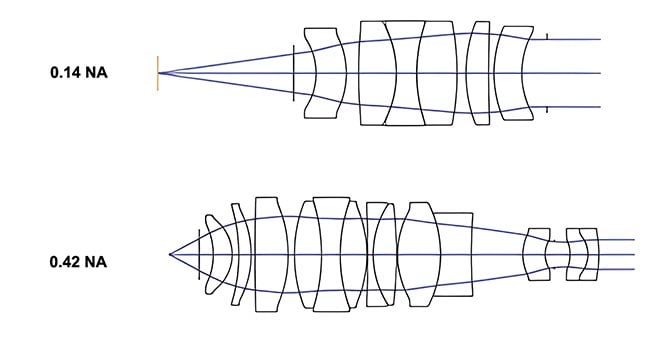
Figure 2. A higher numerical aperture (NA) requires a significantly more complex design with more lens elements compared to the lower NA design. Courtesy of Edmund Optics.

---

Another example of the design challenges presented by these specifications is to compare the complexity of the objective to the tube lens that works with the objective. Both the tube lens and objective need to be diffraction limited, share the same wave band and angular fields of view, and even have the same pupil diameter. But because the NA is a function of the pupil diameter divided by the focal length and the tube lens has a significantly longer focal length than the objective, the NA of the tube lens is factors smaller than that of the objective. This is why the tube lens is typically just a doublet lens that has very loose tolerances.

Wave band

Wave band is often considered by users to be the second most important specification in an objective. Objectives are typically designed for a wide variety of research and clinical applications, so they need to be color-corrected over wide wave bands. Certain applications require wave bands outside the visible range of the spectrum, even including near-infrared or ultraviolet light. The wider the wave band, the greater the occurrence of chromatic aberrations and the more the designer needs to correct for this aberration by adding complexity to the design. The small depth of field in most objectives also means that chromatic aberration must be very small, so as not to cause a focus problem between wavelengths.

This results in designs needing to be not only achromatized but also apochromatic, where the focal length versus wavelength curve has three crossings instead of two to make the total defocus small enough. Apochromatic designs (that bring three colors into focus on the same plane) not only are more complex than achromatic designs with more internal elements, but also have high sensitivities to material tolerances, such as variations in index and Abbe number in the glasses, making manufacturing more expensive and sometimes cost-prohibitive for certain applications (Figure 3).

---

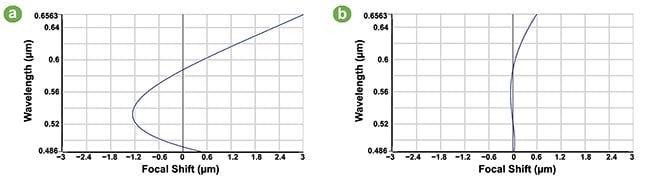
Figure 3. An illustration of achromatic (a) versus apochromatic (b) objective designs, showing that the apochromatic design has 1/6 the chromatic focal shift of the achromatic design. Courtesy of Edmund Optics.

---

In addition to the imaging performance being driven by the wave band, often microscope objectives must serve as the illumination path for the light arriving at the objective. For applications such as fluorescence microscopy, the objective must transmit ultraviolet or short-wavelength light onto the object as well as image the fluoresced longer-wavelength light. This illumination path does not require aberration correction, but it does require that the materials transmit the short wavelengths. This can reduce the available options of glass materials that the designer can use, making aberration correction much more difficult.

Field of view

The third specification that drives the complexity of the objective design is the field of view. Specifically, angular field of view drives the aberrations in the objective: Angular field of view (the angle from the objective extending outward) drives coma, astigmatism, field curvature, and lateral color aberrations, which the designer must optimize in the design of the objective to correct. Angular field of view affects the size of the optical system. For a fixed image size, such as when an eyepiece field stop diameter is already defined or a sensor size on a camera is defined, the angular field of view will define the focal length of the tube lens using the following equation:


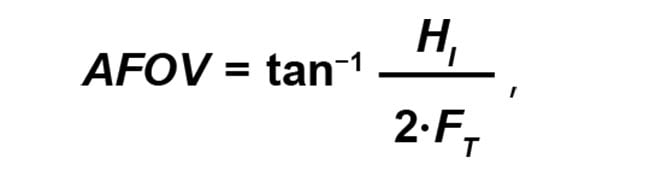
where AFOV is the angular field of view, HI is the diameter of the field stop or the diagonal size of the sensor, and FT is the focal length of the tube lens. For large field stops, which limit the field size, a long focal length tube lens is needed. This drives the length of the overall image system to increase because the tube lens focal length is the most significant length in the system. To shorten the system, either a smaller field stop or a wider angular field of view is needed.

Typically, microscope objectives have a small AFOV of ~4°. By keeping the AFOV a small angle close to paraxial, significantly less aberration content results, making it easier to control the field-related aberrations in the design.

The ultimate choice

Pushing any one of these three key specifications to be large makes the objective design increasingly complex. Pushing any two to be large makes a design very difficult, but possible. However, it is impractical to push all three to be large. When specifying an objective, one specification must be kept low to make the design feasible. To keep the objective cost-effective, two specifications must be kept low.

NA is almost always one of the specifications that are made to be larger. Wavelength range is sometimes needed to be kept broad to capture details for medical diagnostics, for example, but when it is possible to use a narrow wave band by using filters or narrowband illumination, then the complexity of the design can be reduced. AFOV can also be decreased to maintain a lower level of complexity. AFOV is typically the specification that is intentionally kept small, but in systems in which size is very important, increasing AFOV while reducing wave band and NA is an option to reduce the overall size of the system.

Understanding these trade-offs can help guide those searching through available options. And by describing the type of samples that will be inspected, a supplier can determine the required resolution or desired outcomes. Any working distance or other system constraint provides helpful context to the component supplier to help to identify the best solutions; understanding the trade-offs between aperture, wave band, and field of view is valuable context for setting this conversation up for success.

Meet the author

Jeremy Govier is the senior principal engineer at Edmund Optics’ Tucson, Arizona, office. He leads a team of advanced application engineers that support custom optical assembly development. He holds a graduate certificate in project management from the New Jersey Institute of Technology and a bachelor’s degree in optics from the University of Rochester; email: [email protected].

More news & features