Integrating a wavefront sensor into a microscope allows phase data to be extracted, which can provide localized insights into metabolism and treatment progress, without complex instrumentation.
Benoit Wattellier, Phasics Imaging
Examining the cycle of life through the lens of a microscope is a fundamental practice in biology. As researchers have delved deeper into the microscopic world, a pursuit for higher resolution has ensued, leading to discoveries about the smallest constituents within cells. It was during this quest that the significance of light’s informational content became apparent, and some of the latest innovations in quantitative phase microscopy are tapping into this in a variety of applications.
Quantitative phase imaging (QPI) produces a slice of tumorous mouse skin at 40× magnification (scanned and stitched to obtain a 5000 × 5000 pixel image). Courtesy of Phasics.
Phase information provided valuable insights into cellular characteristics, such as dry mass and metabolic activity.
Frits Zernike’s pioneering work in phase contrast microscopy during World War II (winning the Nobel Prize in 1953) unveiled a variety of previously unseen details, surpassing the limitations of traditional bright-field microscopy. This innovation continued with the introduction of fluorescence microscopy, which greatly enhanced optical observation by selectively highlighting pertinent information, thus improving specificity and clarity for the observer.
While phase microscopy initially lacked this advantageous feature, its inherent potential began to emerge as scientists recognized its role beyond mere contrast enhancement. It became evident that phase information provided valuable insights into cellular characteristics, such as dry mass and metabolic activity (Figure 1). However, it wasn’t until the late 20th century that this potential was fully realized with the advent of digital holography, a sophisticated application of Mach- Zehnder interferometry tailored for microscopy1.
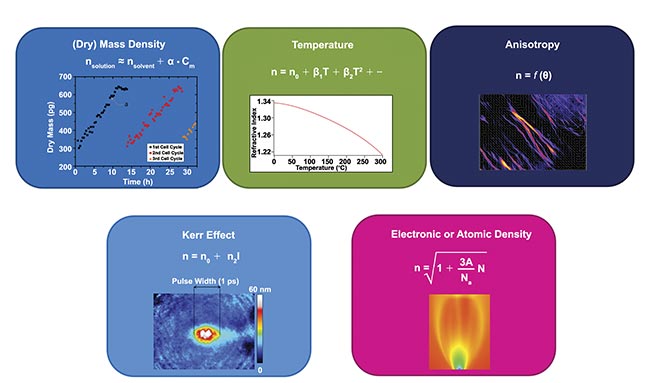
Figure 1. Physical processes that influence the refractive index in transparent media and hence the light phase. Some of them find applications in biology — namely, density, anisotropy, and temperature. Courtesy of Phasics.
With the emergence of quantitative phase imaging (QPI), the inherent advantages of phase information were revealed. This technique was shown to not only provide the clarity researchers sought but also enabled precise quantitative analysis, marking a milestone in the use of microscopic systems.
Incorporating wavefront sensing
To enable the adoption of QPI in biology laboratories, two significant challenges must be addressed. The first hurdle involves navigating the intricacies of interferometry, which is highly sensitive to factors such as alignment and temperature fluctuations. The second challenge lies in developing tailored analysis tools and protocols optimized for biological applications.
One promising solution to the complexity of interferometry is wavefront sensing. A wavefront sensor is a device capable of recording both the phase and intensity of incoming light beams. Initially used for characterizing optics and laser beams, wavefront sensors have now found application in microscopy. One proposal involved replacing the conventional camera at the exit port of a standard microscope with a wavefront sensor, effectively transforming it into a “phase camera”2. However, it is crucial to note that this instrument captures not only light phase but also intensity, which holds a close relationship with object transmission.
Through experimentation, researchers from Institut Fresnel and Phasics collaborated to demonstrate the feasibility of QPI using a halogen light source with Koehler illumination (distributed evenly throughout a sample). This approach leveraged quadriwave lateral shearing interferometry (QLSI), a technology pioneered by Jérôme Primot, in which a diffraction grating is placed in front of a camera3. Its initial implementation on a microscope was conducted by Pierre Bon et al.2.
This article will delve into the intricacies of QLSI and elucidate how QPI, facilitated by wavefront sensors, serves as a robust tool for probing cellular metabolism and responses to external stressors, such as toxins. It will also showcase how incorporating the concept of retardance, exploiting the phase’s dependence on polarization, adds crucial specificity to QPI. This enhancement enables researchers to delineate collagen fibers within cancerous tissues, offering valuable insights into disease pathology.
Basics of QLSI
QLSI operates on the principle that when a light ray encounters a change in refractive index, not only is the speed of light altered but also the direction of the ray. This phenomenon is known as refraction. In other terms, since optical path difference (OPD, or phase when expressed in fractions of the wavelength) represents the accumulation of refractive index along the propagation path, understanding the OPD or the phase equates to understanding the directions of ray propagation. To delve deeper, the unit vectors of the rays are identical to the gradients of the OPD.
In contrast to digital holography, which directly measures phase differences with a reference wave, QLSI focuses on capturing ray directions and subsequently reconstructing the phase by integrating their gradients.
Consequently, collagen organization within melanoma tumors of varying grades could be analyzed, revealing distinct patterns: random organization in healthy tissues versus directional alignment in advanced tumors.
The process begins with the principle of the Hartmann wavefront sensor, which measures the wavefront shape as well as the intensity distribution of the incident beam (Figure 2). The microscopic image is sampled using a periodic grid of apertures, and the projection of this grid onto a CMOS sensor is observed. When all rays propagate uniformly, indicating homogeneous phase information within the sample, the resulting projection forms a periodic grid of dots mirroring the physical grid’s period.
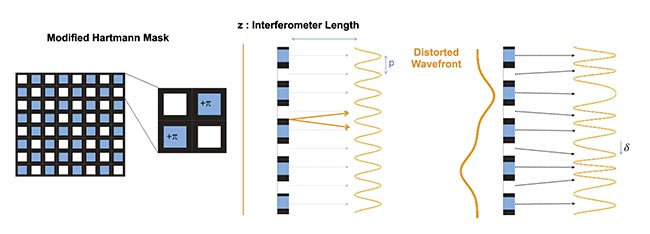
Figure 2. A principle of quadriwave lateral shearing interferometry (QLSI) based on the modified Hartmann mask (MHM) diffractive optics. Courtesy of Phasics.
However, if the image contains variations in mass densities across cellular structures, such as the extracellular environment, cytoplasm, and nucleus, the rays refract, causing local deformations in the projected grid. This deformation is directly proportional to the ray direction. Primot conceptualized this method, extending the Shack-Hartmann variant into multiwave lateral shearing interferometry (MLSI). He refined the grid of apertures, starting from the simplest sinusoidal transmittance grid, which, due to practical limitations in optics, necessitated an approximation known as the modified Hartmann mask. This mask comprises both a magnitude mask, mimicking the Hartmann grid, and a phase mask, introducing a π-shift in every other aperture.
The resulting pattern is modeled as the interference of four replicates of the incident beam, hence the technique’s name. An outstanding advantage of this method compared to other MLSI techniques lies in its requirement of only a few pixels to accurately quantify the initial grid’s deformation. This innovation facilitated the realization of phase images using a wavefront sensor.
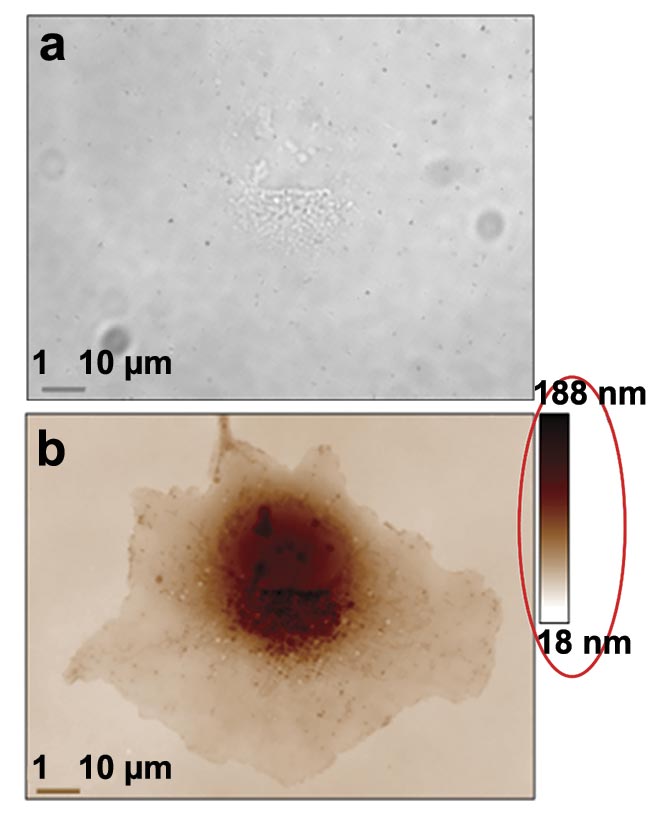
With a plug-and-play QPI camera, these capabilities can be harnessed for biological applications (Figure 3). Two properties of light phase provide valuable insights regarding cell metabolism and the structural arrangement of collagen fibers within cancerous tumors.
 /
/
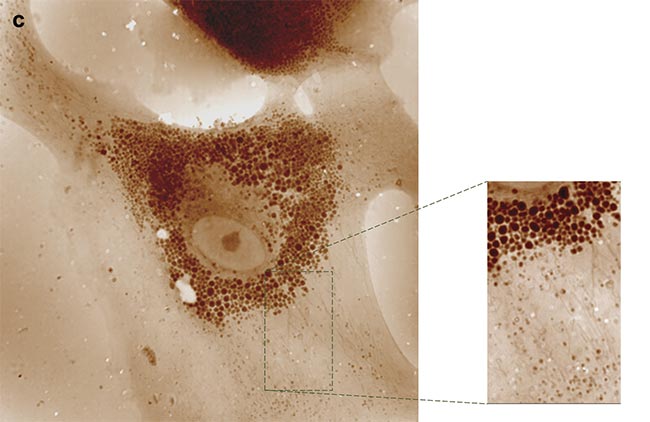
Figure 3. Two examples of quantitative phase imaging (QPI). A transmission image of a COS-7 cell at 100× magnification and 1.3 numerical aperture (NA). Its contrast is very low and only nucleoli are detectable (a). A phase image in which all the cell components are highly contrasted. The red ellipse is here to draw attention to the quantitative aspect of the image (b). A 5.5-MP QPI image of an astrocyte at 100× magnification and 1.3 NA, in which organelles can be tracked upon their trafficking network (c). Courtesy of Phasics and Institut Fresnel.
Tracking cellular changes
During the cell cycle, particularly the G1 phase when most of the growth occurs, cells undergo synthesis of various proteins essential for growth, proliferation, and communication with their environment. This process continues until the cell mass reaches a level specific to its phenotype. Subsequently, in the S phase, DNA and associated proteins are duplicated in preparation for mitosis, during which genetic information is equally distributed between the two daughter cells. While proteins and organelles within the cytoplasm are also parted, this division may not necessarily be equal. However, by the end of the subsequent G1 phase, the mass of both daughter cells should be relatively similar.
The growth rate and final mass value remain consistent for cells within the same lineage and environment. However, exposure to toxins or nutrient deficiencies can alter the growth rate, potentially leading to cell death.
To study the cytotoxicity of a chemical, a common protocol involves seeding petri dishes with cells, adding the chemical, and allowing several cell divisions to occur before counting the remaining cells. However, this process is time-consuming, particularly for human cells with cell cycles lasting >20 h. If the cell mass growth rate could be directly monitored, there could be a rapid assessment of the effects of the chemical, potentially within a much shorter time frame than several cell divisions. Here, QPI can show its value for viewing cellular reactions.
In the 1950s, Robert Barer demonstrated that the refractive index of a solute is the sum of the solvent refractive index and a term proportional to the dry mass density (the cell components’ mass, excluding water). For proteins and most other cell components, this proportionality factor (also known as the specific refractive index) is approximately constant, typically ~0.18 μm3/pg. Considering the sample is illuminated by a plane wave, the accumulated phase (the OPD) is the summation of refractive indices along the line of sight. By integrating the phase over the cell surface, the resulting optical volume is proportional to the total cell dry mass. This characteristic renders QPI a very useful tool for studying mass changes in cells and intra-cytoplasmic material transfers.
An example of this would be the response of cells to a toxin, such as staurosporine. In an experiment, academic collaborators, in collaboration with the research team, prepared multiple wells in a multi-well plate with varying concentrations of staurosporine and monitored cell growth under these conditions. Initially, individual cells were examined; hundreds of phase images were captured containing cells and they were segmented to isolate each individual cell. These cells were then “weighed” by summing the OPD values within their segmented regions. It is crucial to note that the accuracy of the mass measurement heavily relies on effectively eliminating the contribution from the extracellular environment, of which the density is not perfectly homogeneous. Coverslip optical quality should also be taken into account.
A strategy devised in recent years involved polynomial fitting of the phase image with the segmented cells removed4. The polynomial values were extrapolated to the areas in which cells were detected and subsequently subtracted from the entire phase image. The uncertainty of this method was evaluated based on the mean square error of the polynomial fit. Through this protocol, the growth of each individual cell could be tracked. However, for extended durations and densely populated samples, this approach became overly complex. Upon cell division, tracking both daughter cells was necessary to prevent mass discontinuity resulting from mass partitioning. As cells approached confluence, accurate segmentation became increasingly challenging as they often overlap, leading researchers to consider the bio-dry mass of the entire cell population rather than individual cells. This addressed both issues simultaneously. Mass discontinuities were eliminated as all cells were aggregated, and segmentation only required distinguishing cells from their surroundings.
Biomedical insights
Employing this method, researchers successfully monitored the mass of a cell population for several days even at high densities, observing exponential growth rates that were dependent on staurosporine concentration (Figure 4)5. As depicted in the figure, the effects of this toxin were clearly discernible within hours, laying the foundation for accelerated cytotoxicity assessments.
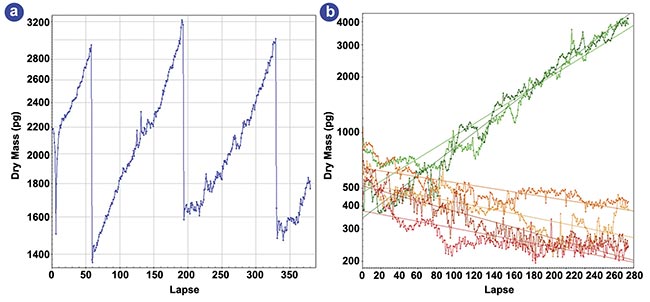
Figure 4. Dry-mass evolution of HEK cells under various staurosporine concentrations. A four-day evolution of the dry mass of a
single HEK cell (a). A six-day evolution of the dry mass of a few hundred HEK cells for various staurosporine concentrations (b).
Adapted with permission from Reference 5.
Concurrently, other research groups used QLSI to monitor cell growth within the context of tailored treatments of cancerous tumors6. Their approach involved exposing tumor cells to various drugs to observe reactions and determine the most effective agents for targeting or eliminating tumor cells, often providing results within hours.
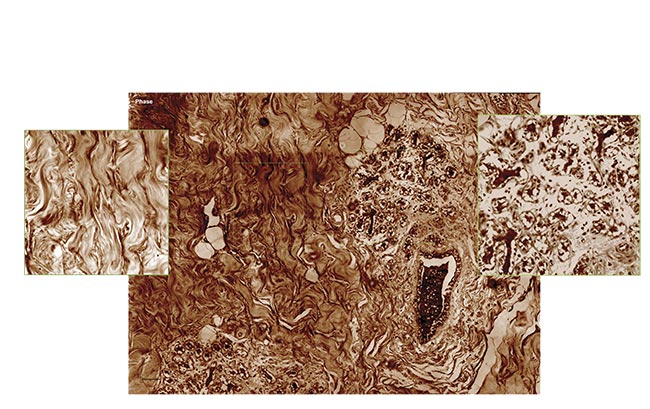
Other innovative approaches are facilitated through QPI with a QLSI wavefront sensor. When cells undergo malignant transformation, they aggregate into tumors, which use collagen fibers as both scaffolding and protection against immune cells or therapeutic agents. Consequently, solid tumors often exhibit fibrosis. In cases of leukemia, fibrosis occurs within the bone marrow, severely impeding hematopoiesis. To comprehend this fibrotic process, researchers typically examine tissue slices stained, for example, with Masson’s trichrome, which highlights collagen. However, this conventional method is laborious, hard to interpret, and entails potential exposure to hazardous chemicals. To expedite and standardize the process, label-free techniques are employed (opening image).
For instance, due to their anisotropic nature, collagen fibers can generate a second harmonic when illuminated with near-infrared short-pulse laser light. This method selectively produces green light only where collagen is present, offering a potent approach for disease prognosis. Nevertheless, generating the second harmonic requires intense light power and sensitive detection equipment. However, anisotropic molecules also manifest a signature in linear optics: birefringence, wherein their refractive index varies with light polarization. This property, describing the oscillation of electric or magnetic fields in space, can be exploited.
By capturing OPD or phase images under various illumination polarizations, differences should be discernible for anisotropic objects, such as collagen fibers, but remain consistent for isotropic objects (Figure 5). A team of researchers demonstrated this phenomenon, providing a straightforward method for detecting collagen and other anisotropic fibers in biological samples7. Consequently, collagen organization within melanoma tumors of varying grades could be analyzed, revealing distinct patterns: random organization in healthy tissues versus directional alignment in advanced tumors. Implementing this protocol merely necessitates inserting a rotating linear polarizer before the tissue sample.
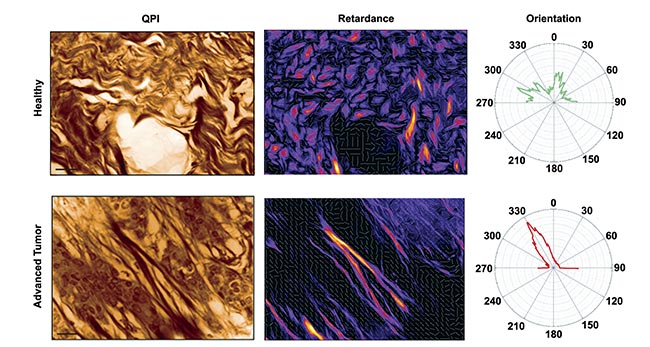
Figure 5. Quantitative phase imaging (QPI) (left) and retardance (right) of a mouse skin tissue for a healthy (top) and advanced tumor (bottom) sample. Only collagen fibers are revealed in the retardance image, whereas cells disappear. Radar representations of fiber
orientation for both conditions are also shown. Courtesy of Phasics.
Next-level application
QPI is burgeoning in research due to user-friendly instrumentation and robust analytical techniques capable of extracting phase information from light. Using a wavefront sensor to generate quantitative phase images simplifies the process, seamlessly replacing a standard CMOS camera in a conventional microscope’s image plane. These ruggedized wavefront sensors, manufactured en masse and engineered for durability, require minimal adaptations for integration into standard microscope setups. QLSI stands out for its high-resolution capabilities, consistently delivering sharp, noise-free, and precise quantitative phase images. This advancement opens avenues for novel biomedical applications.
For instance, in the domain of machine learning, research has demonstrated that incorporating phase information significantly enhances classification accuracy when sorting cell lines. Furthermore, deep learning algorithms have been successfully deployed to detect and analyze the dynamics of the mitochondrial network. Notably, the observation of intracellular organelle dynamics over extended periods is facilitated by QPI, which is impervious to photobleaching, unlike fluorescence imaging.
Lastly, QPI holds promise for applications in cell rejuvenation research. Observations have revealed that senescent cells exhibit lower density compared to standard cells, a distinction easily discernible in quantitative phase images. This capability offers potential insights into the mechanisms underlying cellular aging and rejuvenation.
Meet the author
Benoit Wattellier joined the Lawrence Livermore National Laboratory to work on the NIF Advanced Radiography Program, after obtaining a Ph.D. from École Polytechnique (France) in laser physics. He founded Phasics in 2003 with Marie-Begoña Lebrun, Phasics’ current CEO, to develop quadriwave lateral shearing interferometry, invented by Jérôme Primot. As a CTO, Wattellier leads R&D programs on adaptive optics for lasers and optical metrology; email: [email protected].
References
1. E. Cuche et al. (1999). Digital holography for quantitative phase-contrast imaging. Opt Lett, Vol. 24, No. 5, pp. 291-293.
2. P. Bon et al. (2009). Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells. Opt Express, Vol. 17, No. 15, pp. 13080-13094.
3. J. Primot and N. Guérineau. (2000). Extended Hartmann test based on the pseudoguiding property of a Hartmann mask completed by a phase chessboard. Appl Opt, Vol. 39, No. 31, pp. 5715-5720.
4. S. Aknoun et al. (2015). Living cell dry mass measurement using quantitative phase imaging with quadriwave lateral shearing interferometry: an accuracy and sensitivity discussion. J Biomed Opt, Vol. 20, No. 12, p. 126009.
5. S. Aknoun et al. (2021). Quantitative phase microscopy for non-invasive live cell population monitoring. Sci Rep,
Vol. 11, No. 1. p. 4409.
6. D. Huang et al. (2018). High-speed live-cell interferometry: a new method for quantifying tumor drug resistance and heterogeneity. Anal Chem, Vol. 90, No. 5, pp. 3299-3306.
7. S. Aknoun et al. (2015). Quantitative retardance imaging of biological samples using quadriwave lateral shearing interferometry. Opt Express, Vol. 23, No. 12, pp. 16383-16406.