Optical Research Associates’ Global Synthesis (GS) algorithm has been in use for more than ten years. During that time, the algorithm has been applied to numerous types of problems, and has proved remarkably successful with an approach that is feasible for both large (e.g., >90 variables) and small problems running on personal computers.
Thomas G. Kuper and Thomas I. Harris, Optical Research Associates
Some efforts in global optimization research for optical design center around probabilistic methods such as global search. While promising for small problems with few variables, these methods approach being exponential in the number of variables (N), and the time required to find a solution is:
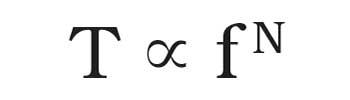
where f is the number of function evaluations for each variable.
The high rate of time scale-up with the number of variables has led to research into algorithmic ways to mitigate the scale-up (such as simulated annealing and genetic algorithms), to the consideration of specialized computing hardware (massively parallel machines) and to the use of more approximate error functions (third-order aberrations, etc.). But it is an uphill battle.
Other characteristics of the algorithm can also affect its usefulness, depending on how the algorithm works. The solutions found may not be locally optimum or may have been optimized using only a reduced set of variables. You may get only one solution (hopefully the global one), and only at the end of a finite run. With only one, you may not know of other possible forms that could have desirable properties not represented in the problem statement (error function and constraints).
Goals for a global optimizer
Some desirable attributes for a global optimizer are:
• Speed/efficiency — It should run on fast but widely available, affordable hardware. Special hardware should not be required. Run times can be long if the gain is great. For example, a process that can be relied upon to produce useful alternative solutions to a complex problem (e.g., zoom lenses) is valuable if it produces results in a few days of continuous running, but a month would be too long. It should have a time scaling law that is better than exponential so that a wide range of problems can be solved, not just simple ones.
• Synthesis/availability — It should produce multiple solutions so that those with interesting but unanticipated characteristics can be pursued. It should produce solutions early in the process not just at the end. This will allow checking the run in case it hasn’t been set up right, and will allow the designer to begin evaluating the more interesting cases before the end. Confidence will be higher that the process will give useful results.
• Feasibility/validity — It should be able to start from any locally optimizable starting point, whether it’s a known optical system or a simplistic starting point. It should find the known multiple solutions for classic and well-documented cases (landscape lens, doublet, triplet, monochromatic quartet, etc.). It should only come up with solutions that are feasible; i.e., that satisfy the constraints and are traceable.
• Broad applicability — It should work with systems that may be centered or decentered, with or without special surfaces (such as aspheric and nonsequential), zoomed or not.
Optical Research Associates’ (ORA) research has met these goals using a different approach. Our work was stimulated by the belief that a process exists that has a low-power scaling law:
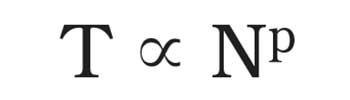
where p is a low number; e.g., 3. If the low-power process and the exponential process require the same time for 10 variables, the low-power process will be faster for 80 variables by a factor of 1018. Clearly, an exponential process does not currently have a chance of solving complex problems, whereas a low-power process does.
The process developed after intensive research and testing, called Global Synthesis, is a proprietary one that involves mathematical analysis and heuristics not found in normal optical optimization algorithms.
The process (including the examples given here) uses Code V error functions and constraints that you would use in regular local optimization to solve the problem. It requires one command to shift into global activity, uses run-length controls normally available to the designer (time limit, error-function target) and can draw each solution configuration as it is found. Each solution is itself a result of Code V local optimization according to normal controls (maximum/minimum cycles and improvement factor).
Examples of Global Synthesis
In the course of developing Global Synthesis we have used a number of test problems to evaluate our progress in improving the speed and reliability of the algorithm.1,2 In this article we will limit our discussion to four examples that illustrate the effectiveness of GS. All computing times are for a 3.6-GHz Pentium 4 computer.
• The wide-angle mapping lens (US Patent No. 3,700,312, invented by L. Berthele of Wild) is a 59-variable problem. Using the locally optimized patent lens as a starting point, a 10-minute run produced 53 alternate design forms, including 19 with error-function values within a factor of 10 of the best design. Note that the error-function value of the best solution was approximately six times smaller than that of the locally optimized patent form. (The square root of the error function is proportional to the average root mean square spot radius, so the spot radius of the best Global Synthesis design was about 2.5 times smaller than the spot radius of the patent.)
Constraints on the designs were constructed to approximately match the limitations faced by the original designer. The patent values for the focal length, the back focal length, overall length, front and rear semidiameters, minimum element center and edge thickness, and maximum element center thickness were used as constraints for the entire run. We also imposed semidiameter constraints on the second and tenth elements (again matching the patent) to help keep the total system weight under control. Since this is a mapping camera lens, very tight constraints on distortion (0.013 percent at full field, 0.0006 percent at two-thirds field) were imposed as well. We added a constraint to ensure that the relative illumination falls off no faster than cos3θ where θ is the semifield angle. This last constraint is often a driver in determining the form of the best solutions for mapping lenses.
For the various Global Synthesis generated design forms, the number of active constraints ranged from a low of 18 to a high of 34.
To verify the quality of these designs, we further studied the locally optimized patent and the two best Global Synthesis designs, performing analyses a typical designer would require to engineer a final design. This included locally optimizing over more fields, fitting to real glasses, evaluating full performance, cost and weight, and tolerancing. The best design was shown to have twice the resolution of the optimized patent, while weighing only two-thirds as much. Figure 1 compares the locally optimized patent (above the center line) with the best Global Synthesis design (below the center line).

Figure 1. Global Synthesis was used to improve this 59-variable, 35-constraint f/4, 90° mapping lens. The location of flint (white) and crown (blue) glasses changes substantially between the patent (top) and the best Global Synthesis (bottom) design. The latter has two times better resolution with tolerancing.
• Our second example is the so-called camera in a can. This is a design problem that was used for the 1994 IODC lens design contest. The goal of this problem is to search for a lens that can resolve 108 Airy discs on a flat image plane, subject to a constraint that the volume of the smallest cylinder enclosing the lens elements and the image surface must be minimum. The lens operates monochromatically at 632.8 nm and must be all-refractive and all-spherical, have no vignetting, use only Schott glasses and work with an object at infinity. In addition, the root mean square wavefront error must be <0.07 waves over the whole field.
The number of lens elements was unspecified, and since Global Synthesis does not vary the number of elements in a given run, a number of runs were needed to investigate the total design space. For the first run, the starting configuration for the camera consisted of two powered elements and six parallel plates of glass. Starting points for subsequent global runs were typically derived from the best solutions of prior runs. Elements were added either by splitting existing elements or by placing plane parallel glass plates in accessible air spaces.
Reasonable constraints on minimum center and edge thicknesses (typically 1 mm) were imposed for all of the Global Synthesis runs except the last one. For the final run these constraints were reduced to 50 µm as we attempted to squeeze the best configuration to get the smallest possible volume. Distortion at the edge of the field was held ≥0 to ensure that we satisfied the minimum field height requirement. The volume was minimized through the use of an inequality constraint with a reasonable target value for each run. Keeping the volume constraint separate from the merit function makes it simpler to determine when designs satisfy the wavefront quality requirement and to eliminate local minimums that represent a compromise between volume and performance.
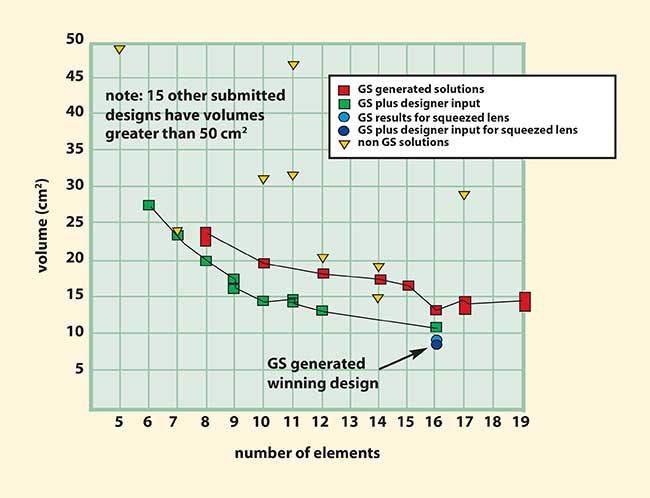
Figure 2. Overall system volume vs. number of elements for the 1994 IODC “camera in a can” lens design problem.
Figure 2 summarizes the results of our design efforts. Global Synthesis runs typically required between 15 and 70 CPU minutes, and used between 41 (eight-element run) and 98 (19-element run) variables. The red squares represent the best Global Synthesis-generated designs. The green squares represent our best efforts to refine the Global Synthesis solutions by cementing, adding or removing elements, by changing the stop location, by adjusting the field and aperture specifications, by fitting to real glasses beyond the glass map limits of the Global Synthesis run, by adjusting optimization weights, and by using any other design insight at our disposal. Finally, the circles indicate results obtained when we squeezed the lens by allowing the minimum edge and center thickness constraints to go to 0.05 mm.
Global Synthesis produced the winning solutions for this design contest, exceeding the performance of 29 other submitted solutions from 19 designers.
• Our third example is the design of an inverted telephoto camera objective (Figure 3). This example is chosen to demonstrate the effectiveness of Global Synthesis for finding new solutions to real design problems.
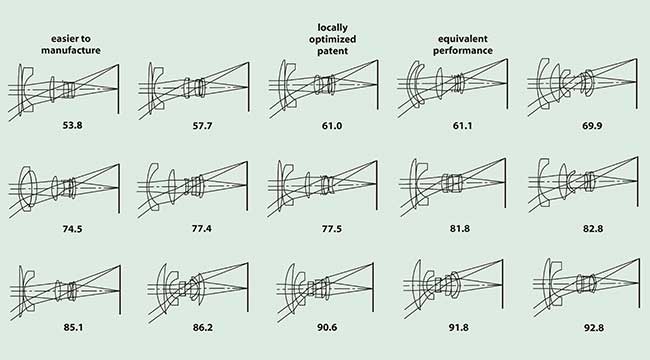
Figure 3. The lens layouts of the 15 best design forms are arranged in order of increasing error functions. The locally optimized patent form is the third best design. Note that the No. 1 design not only is better in terms of error function, but also appears easier to manufacture. The fourth best design matches the patent in performance but has a double meniscus front end. The 12th design is unusual because it is approaching a symmetric form more commonly associated with wide-angle designs than with an inverted telephoto.
The specification for this 36-variable design problem was derived from a patent description (US Patent No. 4,099,850, assigned to Nikon). We generated a set of starting lenses for this problem by first running Global Synthesis, using the locally optimized patent lens as the starting point. From the lenses generated by this first run, we selected nine forms to serve as additional starting points. The error-function values of the 10 starting points ranged from 61 for the patent up to 760. We then ran each version from all 10 starting points. The duration of each run was equivalent to 30 CPU minutes.
We first analyzed results by identifying all the distinct forms with error-function values less than twice the value of the locally optimized patent lens; i.e., less than 120. Of course, many more solutions with higher error-function values were also generated, but these would usually have little value for a designer. A total of 41 distinct forms with error-function values less than 120 were identified.
After identifying and ranking the distinct forms, we analyzed the output of each run to determine how many of the distinct forms were found, and also to determine how much run time was required to find each successive form. The results were then averaged over the 10 runs for Global Synthesis (Figure 4). On average, about 60 percent of the known forms are discovered by a single half-hour run.
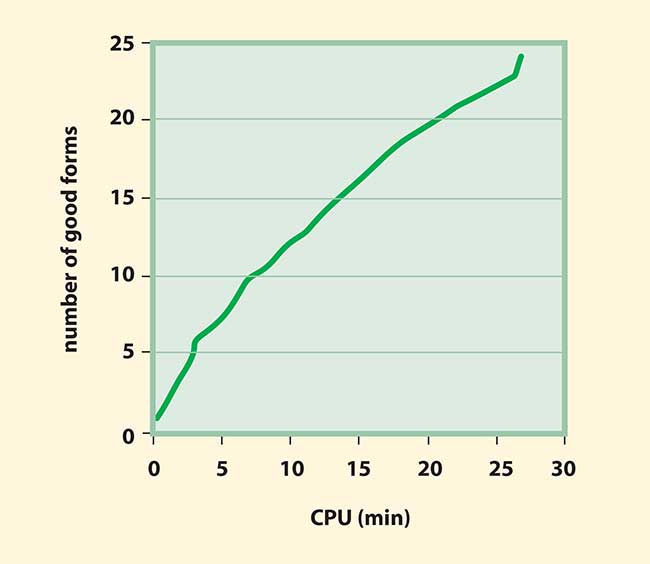
Figure 4. The average number of good distinct forms (those with error-function values less than two times that of the locally optimized patent example) discovered by GS vs. the required CPU time shows a nearly linear increase in forms with time.
• Our final example shows the behavior of Code V for zoomed systems.3 Once again the problem specification was derived from a patent description (US Patent No. 5,398,135 assigned to Ricoh Co. Ltd. in 1993). Our goal was to show that GS can find good solutions for zoom lenses, even from an arbitrary starting point that starts out with the wrong group power distribution.
Figure 5 shows a first position layout for the starting point lens, and Figure 6 shows first position layouts for selected generated solutions, illustrating the point that designs with all possible group power distributions were found. The best design discovered by GS in a two-hour run is the locally optimized patent form.
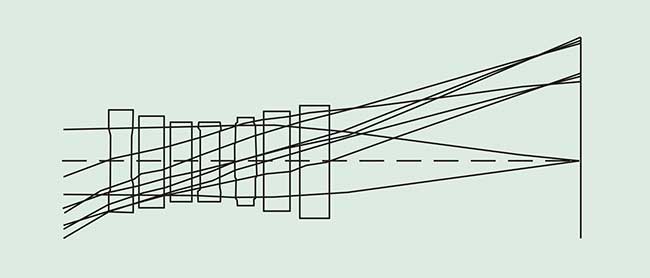
Figure 5. Starting (- +) configuration before local optimization to satisfy constraints.
Where do we go from here?
Experiences with our approach to global optimization have led us to regard it as a powerful added tool for the optical engineer. To get the most out of this new capability, however, designers must learn to develop global rather than local optimization strategies. For example:
• Simplified error functions inadequate for final design (e.g., fewer fields, coarser ray grids or D minus d color modeling) may be used to find design forms that are later refined through local optimization with a more complete error function, thereby speeding up the global part of the process and simplifying the final selection process.
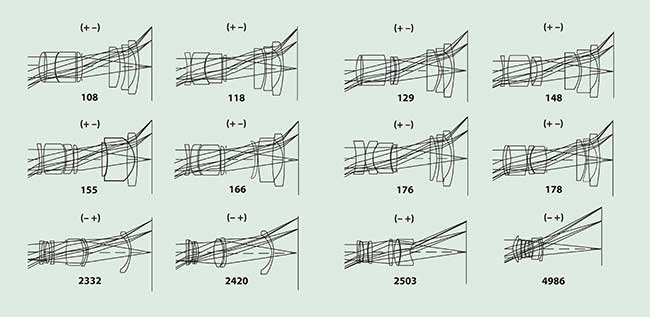
Figure 6. First position layouts for selected GS generated zoom lens designs. The number below each form is the error-function value.
• Looser convergence criteria can be specified so the program spends less time fine tuning the designs and more time searching different regions of solution space.
• Omit noncritical constraints that may apply to only a few of the configurations but not the ultimate goal (e.g., ray-height constraints and configuration-dependent packaging constraints).
• Using weighted constraints rather than Lagrange multiplier-type constraints for EFL and possible distortion in zoomed systems.
• Specify angle of incidence constraints to control the number of ray failures during the global search.
Much work remains to be done in global optimization for optical design, but it is our hope that the availability of a practical approach will stimulate greater interest in research and increased understanding of optical design.
References
1. Kuper, T. and T. Harris (January 1992). A New Look at Global Optimization for Optical Design, PHOTONICS SPECTRA, 26:1:151-160.
2. Kuper, T. and T. Harris. Global Optimization — An Emerging Technology, Proc. SPIE. Sept. 14-18, 1992, Berlin, Germany. 1780:14-28.
3. Kuper, T. and T. Harris. A Practical Strategy for Global Optimization of Zoom Lenses, International Optical Design Conference. June 5-12, 1998, Kona, Hawaii.