Photonics HandbookOptics
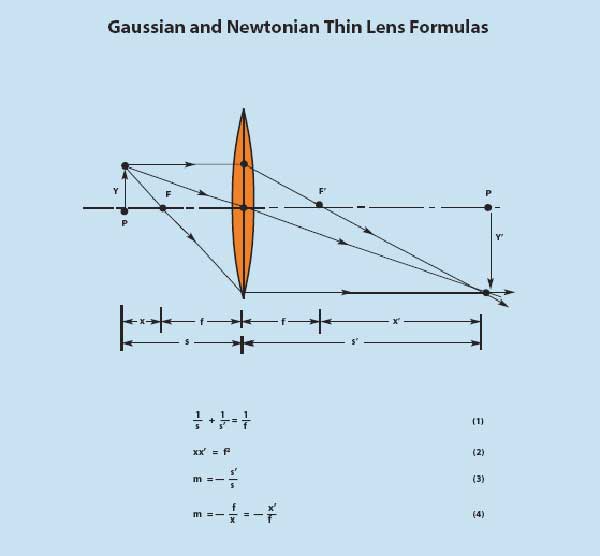
Gaussian and Newtonian Thin Lens Formulas
Four important equations from which the image distance and the lateral magnification can be computed for an object at any arbitrary distance from a thin lens.
Equation (1) is known as the Gaussian form of the lens equation, after the mathematician Karl F. Gauss. Equation (2), first derived by Sir Isaac Newton, is the Newtonian form of a lens equation. The Gaussian form is probably more familiar, but the Newtonian equation is algebraically simpler. Notice that in the former equation object and image distances s and s’ are measured from the center of a thin lens, while in the latter, object and image distances x and x’ are measured from the focal points F and F’.
The lateral magnification m can be expressed either in terms of s and s’, by equation (3), or in terms of x, x’ and f, by equation (4).
/Buyers_Guide/Walker_Associates/c15921